题目内容
函数f(x)=
+lg(2-x-1)的定义域为( )
| -2 | ||
|
| A、(-5,+∞) |
| B、[-5,+∞) |
| C、(-5,0) |
| D、(-2,0) |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据函数成立的条件,即可求出函数的定义域.
解答:
解:要使函数有意义,x满足:
,
解得-5<x<0.
故选:C.
|
解得-5<x<0.
故选:C.
点评:本题考查对数函数的定义域,解题时要认真审题,注意对数函数性质的灵活运用.

练习册系列答案
相关题目
直线λx+y+λ-2=0不过第三象限,则λ的取值范围是( )
| A、[0,1] |
| B、[0,2] |
| C、(-∞,4] |
| D、[4,+∞) |
下列关系中正确的是( )
A、log76<ln
| ||
B、log3π<ln
| ||
C、ln
| ||
D、ln
|
已知集合A={x|x2-2x-3<0},B={y|1≤y≤4},则下列结论正确的是( )
| A、A∩B=∅ |
| B、(∁UA)∪B=(-1,+∞) |
| C、A∩B=(1,4] |
| D、(∁UA)∩B=[3,4] |
若关于x的方程25-|x+1|-4×5-|x+1|=m有实根,则实数m的取值范围是( )
| A、m<0 | B、m≥-4 |
| C、-4≤m<0 | D、-3≤m<0 |
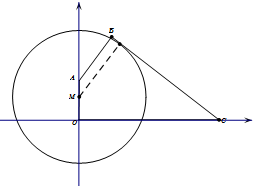 已知四边形OABC中,OA⊥OC,AB⊥BC,且OA=6,OC=17,tan∠BCO=
已知四边形OABC中,OA⊥OC,AB⊥BC,且OA=6,OC=17,tan∠BCO= 如图是一个几何体的三视图(单位:cm),计算这个几何体的体积与表面积.
如图是一个几何体的三视图(单位:cm),计算这个几何体的体积与表面积.