题目内容
已知命题P:x=1是ax2+bx+c=0的一个根,命题q:a+b+c=0,则p是q的( )条件.
| A、充分非必要 |
| B、必要非充分 |
| C、充要 |
| D、既不充分也不必要 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:分别证明充分性和必要性,结合二次函数的性质得到答案.
解答:
证明:先证明充分性:
∵x=1,∴ax2+bx+c=a+b+c=0,是充分条件,
再证明必要性:
∵a+b+c=0,∴x=1是ax2+bx+c=0的一个根,是必要条件,
故选:C.
∵x=1,∴ax2+bx+c=a+b+c=0,是充分条件,
再证明必要性:
∵a+b+c=0,∴x=1是ax2+bx+c=0的一个根,是必要条件,
故选:C.
点评:本题考查了充分必要条件,是一道基础题.

练习册系列答案
相关题目
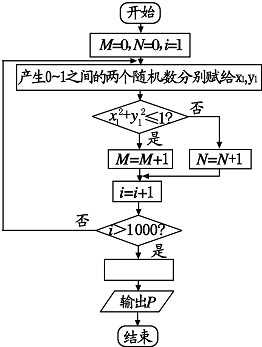
如图所示,使用模拟方法估计圆周率值的程序框图,P表示估计的结果,则图中空白框内应填入P=( )

A、
| ||
B、
| ||
C、
| ||
D、
|