Question

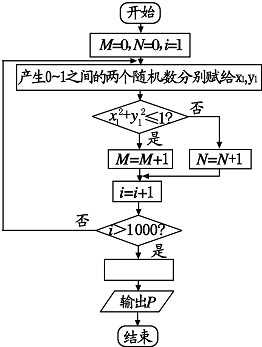
如图所示，使用模拟方法估计圆周率值的程序框图，P表示估计的结果，则图中空白框内应填入P=（　　）

• A、

  M

  1000

• B、

  1000

  M

• C、

  4M

  1000

• D、

  1000

  4M

Answer 1

考点：程序框图

专题：算法和程序框图

分析：由题意以及框图的作用，直接推断空白框内应填入的表达式．

解答： 解：法一：由题意以及程序框图可知，用模拟方法估计圆周率π的程序框图，M是圆周内的点的次数，当i大于1000时，
圆周内的点的次数为4M，总试验次数为1000，
所以要求的概率

4M

1000

，
所以空白框内应填入的表达式是P=

4M

1000

．
故选：C．
法二：随机输入xi∈（0，1），yi∈（0，1）
那么点P（xi，yi）构成的区域为以O（0，0），A（1，0），B（1，1），C（0，1）为顶点的正方形．

判断框内x²_i+y²_i≤1，
若是，说说明点P（x_i，y_i）在单位圆内部（

1

4

圆）内，并累计记录点的个数M
若否，则说明点P（x_i，y_i）在单位圆内部（

1

4

圆）外，并累计记录点的个数N
第2个判断框 i＞1000，是进入计算

此时落在

1

4

单位圆内的点的个数为M，一共判断了1000个点
那么

1

4

圆的面积/正方形的面积=

M

1000

，
即

1

4

π1²÷1=

M

1000

∴π=

4M

1000

（π的估计值）
即执行框内计算的是P=

4M

1000

．
故选：C．

点评：本题考查程序框图的作用，考查模拟方法估计圆周率π的方法，考查计算能力．