题目内容
将函数f(x)=lgx的图象向左平移1个单位,再将位于x轴下方的图象沿x轴翻折得到函数g(x)的图象,若实数m,n(m<n)满足g(m)=g(-
),g(10m+6n+21)=4lg2,则m-n的值是( )
| n+1 |
| n+2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
考点:函数的图象与图象变化
专题:函数的性质及应用
分析:根据函数图象的平移变换法则及对折变换法则,可得变换后g(x)=|lg(x+1)|,进而根据m<n满足g(m)=g(-
),g(10m+6n+21)=4lg2,构造方程组,解方程可得答案.
| n+1 |
| n+2 |
解答:
解:将函数f(x)=lgx的图象向左平移1个单位,可得函数f(x)=lg(x+1)的图象;
再将位于x轴下方的图象沿x轴翻折得到函数g(x)=|lg(x+1)|的图象,
由g(m)=g(-
),可得(m+1)•(1-
)=1或m+1=1-
,
若(m+1)•(1-
)=1时,m=n+1,这与m<n矛盾,
故m+1=1-
,即m=-
,
由g(10m+6n+21)=4lg2,可得|lg(10m+6n+21+1)|=lg16,
故10m+6n+22=16或10m+6n+22=
,
即-10×
+6n+22=16…①或-10×
+6n+22=
…②,
解①得n=-1,m=0这与m<n矛盾,
或n=-
,m=-
,此时m-n=-
,
解②得方程无解,
综上所述,m-n=-
,
故选C
再将位于x轴下方的图象沿x轴翻折得到函数g(x)=|lg(x+1)|的图象,
由g(m)=g(-
| n+1 |
| n+2 |
| n+1 |
| n+2 |
| n+1 |
| n+2 |
若(m+1)•(1-
| n+1 |
| n+2 |
故m+1=1-
| n+1 |
| n+2 |
| n+1 |
| n+2 |
由g(10m+6n+21)=4lg2,可得|lg(10m+6n+21+1)|=lg16,
故10m+6n+22=16或10m+6n+22=
| 1 |
| 16 |
即-10×
| n+1 |
| n+2 |
| n+1 |
| n+2 |
| 1 |
| 16 |
解①得n=-1,m=0这与m<n矛盾,
或n=-
| 1 |
| 3 |
| 2 |
| 5 |
| 1 |
| 15 |
解②得方程无解,
综上所述,m-n=-
| 1 |
| 15 |
故选C
点评:本题考查的知识点是函数图象的变换法则,方程思想,本题运算量比较大,分类比较麻烦,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 一个几何体的三视图如图所示,其中正视图是正三角形,则几何体的外接球的表面积为( )
一个几何体的三视图如图所示,其中正视图是正三角形,则几何体的外接球的表面积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
设F为抛物线y2=8x的焦点,A,B,C为该抛物线上三点,若
+
+
=
,则|
|+|
|+|
|=( )
| FA |
| FB |
| FC |
| 0 |
| FA |
| FB |
| FC |
| A、6 | B、9 | C、12 | D、16 |
已知平行四边形ABCD中,
=(2,8),
=(-3,4),则
的坐标为( )
| AD |
| AB |
| AC |
| A、(-1,-12) |
| B、(-1,12) |
| C、(1,-12) |
| D、(1,12) |
已知复数z满足
=i(i为虚数单位),则z的值为( )
| 1+z |
| 1-z |
| A、i | B、-i | C、1 | D、-1 |
若变量x,y满足
,实数z是2x和-4y的等差中项,则z的最大值等于( )
|
| A、1 | B、2 | C、3 | D、4 |
已知函数f(x)=x2-x-3,则函数g(x)=f(f(x))-x所有零点的和为( )
| A、-2 | B、0 | C、2 | D、4 |
已知{an}为等比数列,下面结论中正确的是( )
| A、a1+a3≥2a2 |
| B、若a1=a3,则a1=a2 |
| C、a12+a32≥2a22 |
| D、若a3>a1,则a4>a2 |
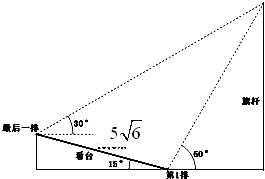 某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15°的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为5
某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15°的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为5