题目内容
圆x2+y2+3x-2y-1=0的圆心坐标为 ,半径为 .
考点:圆的一般方程
专题:计算题,直线与圆
分析:根据圆的一般式方程改写成圆的标准方程,进而由圆的标准方程得到圆的圆心坐标与圆的半径.
解答:
解:由题意可得:圆的标准方程为:(x+1.5)2+(y-1)2=4.25,
所以圆的圆心为(-1.5,1),半径为
.
故答案为:(-1.5,1);
.
所以圆的圆心为(-1.5,1),半径为
| ||
| 2 |
故答案为:(-1.5,1);
| ||
| 2 |
点评:解决此类问题的关键是熟练掌握圆的一般方程与标准方程之间的相互转化,并且结合正确的运算.

练习册系列答案
相关题目
若直线(a2+4a+3)x+(a2+a-6)y-6=0与x-2y-1=0垂直,则a等于( )
| A、.5 | B、.5或-3 |
| C、.-3 | D、不存在 |
下列说法中错误的是( )
A、若f(x)=x2-3,g(x)=
| ||||||
| B、若函数的定义域只含有一个元素,则该函数的值域也只含有一个元素 | ||||||
| C、函数y=2x(x∈N)的图象是一条直线 | ||||||
D、y=
|
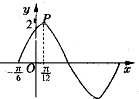 已知函数f(x)=2sin(ωx+φ),(ω>0,φ∈(0,
已知函数f(x)=2sin(ωx+φ),(ω>0,φ∈(0,