题目内容
若直线（a2+4a+3）x+（a2+a-6）y-6=0与x-2y-1=0垂直，则a等于（ ）
| A、.5 | B、.5或-3 |
| C、.-3 | D、不存在 |
考点：直线的一般式方程与直线的垂直关系
专题：直线与圆
分析：利用直线垂直与斜率的关系即可得出．
解答：
解：∵直线（a2+4a+3）x+（a2+a-6）y-6=0与x-2y-1=0垂直，
∴直线（a2+4a+3）x+（a2+a-6）y-6=0的斜率存在，∴k1=-
．
x-2y-1=0的斜率k2=
．
∴k1k2=-
×
=-1．
化为a2-2a-15=0，
解得a=5或-3．
故选：B．
∴直线（a2+4a+3）x+（a2+a-6）y-6=0的斜率存在，∴k1=-
| a2+4a+3 |
| a2+a-6 |
x-2y-1=0的斜率k2=
| 1 |
| 2 |
∴k1k2=-
| a2+4a+3 |
| a2+a-6 |
| 1 |
| 2 |
化为a2-2a-15=0，
解得a=5或-3．
故选：B．
点评：本题考查了直线垂直与斜率的关系，属于基础题．
练习册系列答案
应用题作业本系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
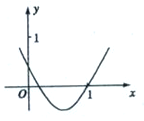函数f（x）=x2-bx+a的图象如图所示，则函数g（x）=lnx+f′（x）的零点所在的区间是（ ）A、(
| ||||
B、(
| ||||
| C、（1，2） | ||||
| D、（2，3） |
已知椭圆的长轴、短轴、焦距长度之和为8，则长半轴的最小值是（ ）
| A、4 | ||
B、4
| ||
C、4(
| ||
D、2(
|
设函数y=f（x）与函数y=g（x）的图象如图所示，则函数y=f（x）•g（x）的图象可能是下面的（ ）
