题目内容
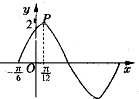已知函数f（x）=2sin（ωx+φ），（ω＞0，φ∈（0，| π |
| 2 |
| π |
| 2 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的求值,三角函数的图像与性质
分析：首先根据函数的图象确定函数的解析式，即确定函数中ω和Φ的值，进一步求出函数的值．
解答：
解：根据函数的图象得：T=π
所以：
=π，
求得：ω=2
当x=
时，f（x）=2
解得：Φ=
函数f（x）=2sin（2x+
）
当x=
时，f（
）=-
故答案为：-
所以：
| 2π |
| ω |
求得：ω=2
当x=
| π |
| 12 |
解得：Φ=
| π |
| 3 |
函数f（x）=2sin（2x+
| π |
| 3 |
当x=
| π |
| 2 |
| π |
| 2 |
| 3 |
故答案为：-
| 3 |
点评：本题考查的知识要点：利用正弦型函数图象求ω和Φ的值，进一步利用函数的解析式求函数的值．
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
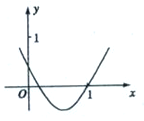函数f（x）=x2-bx+a的图象如图所示，则函数g（x）=lnx+f′（x）的零点所在的区间是（ ）A、(
| ||||
B、(
| ||||
| C、（1，2） | ||||
| D、（2，3） |