题目内容
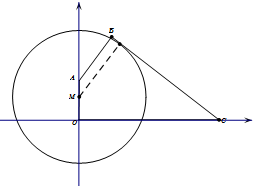已知四边形OABC中，OA⊥OC，AB⊥BC，且OA=6，OC=17，tan∠BCO=| 4 |
| 3 |
（1）求AB的长；
（2）OM多长时，圆M的面积最大？
考点：直线与圆的位置关系
专题：直线与圆
分析：（1）连结OA，在Rt△AOC中求AC和tan∠ACO，然后求tan∠ACB=tan（∠BCO-∠ACO），在Rt△ABC中，求AB和BC，即可．（2）根据题目条件设圆的半径为R，列不等式求解R范围，当R最大时求OM．
解答：
解（1）连结OA，在Rt△AOC中，AC=
=5
，tan∠ACO=
，
则tan∠ACB=tan（∠BCO-∠ACO）=
，
在Rt△ABC中，设AB=a，BC=b，则有
，解得BC=15，AB=10，
（2）设圆的半径为R，由题意可求OM=
-
R．根据两点O与A到圆M上任意一点的距离均不小于8．
得14-R≤
-
R≤R-8⇒10.5≤R≤13
当OM=1时，R最大为13．
| 172+62 |
| 13 |
| 6 |
| 17 |
则tan∠ACB=tan（∠BCO-∠ACO）=
| 2 |
| 3 |
在Rt△ABC中，设AB=a，BC=b，则有
|
（2）设圆的半径为R，由题意可求OM=
| 68 |
| 3 |
| 5 |
| 3 |
得14-R≤
| 68 |
| 3 |
| 5 |
| 3 |
当OM=1时，R最大为13．
点评：本题考察圆与直线的位置关系，其中相切为考察重点，可构造相应三角形求解．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=
+lg(2-x-1)的定义域为（ ）
| -2 | ||
|
| A、（-5，+∞） |
| B、[-5，+∞） |
| C、（-5，0） |
| D、（-2，0） |
集合M={-2，0，1，2}，N={x|x2-x＞0}，则M∩N=（ ）
| A、{-2，1，2} |
| B、{0，2} |
| C、{-2，2} |
| D、[-2，2] |
已知函数f（x）在[0，+∞）上可导，其导函数记作f′（x），f（0）=-2，且f（x+π）=
f（x），当x∈[0，π）时，f′（x）•cos2x＞f（x）•sin2x-f′（x），若方程f（x）+knsecx=0在[0，+∞）上有n个解，则数列{
}的前n项和为（ ）
| 1 |
| 2 |
| n |
| k2n |
| A、（n-1）•2n+1 | ||
| B、（n-1）•2n+1+2 | ||
| C、n•2n-1 | ||
D、
|
设Sn为数列{an}的前n项和，an=1+2+22+…+2n-1，则Sn的值为（ ）
| A、2n-1 |
| B、2n-1-1 |
| C、2n-n-2 |
| D、2n+1-n-2 |