题目内容
已知函数f(x)在[0,+∞)上可导,其导函数记作f′(x),f(0)=-2,且f(x+π)=
f(x),当x∈[0,π)时,f′(x)•cos2x>f(x)•sin2x-f′(x),若方程f(x)+knsecx=0在[0,+∞)上有n个解,则数列{
}的前n项和为( )
| 1 |
| 2 |
| n |
| k2n |
| A、(n-1)•2n+1 | ||
| B、(n-1)•2n+1+2 | ||
| C、n•2n-1 | ||
D、
|
考点:数列的求和
专题:计算题,函数的性质及应用,导数的综合应用,等差数列与等比数列
分析:由于f(0)=-2,且f(x+π)=
f(x),则f(π)=
f(0)=-1,f(2π)=
f(π)=-
,f(3π)=-
,
…,f(nπ)=-(
)n-1.再由导数的积的运算法则和二倍角公式,得到f(x)cosx的单调性和极值,由条件可得,kn=-f(x)cosx在[0,+∞)上有n个解,k1=-f(0)cos0=2,k2=-f(π)cosπ=-1,…,kn=-f((n-1)π)cos(n-1)π,则有k2n=(
)n-1,即有
=n•2n-1,再运用错位相减法,即可得到前n项和.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
…,f(nπ)=-(
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| k2n |
解答:
解:由于f(0)=-2,且f(x+π)=
f(x),
则f(π)=
f(0)=-1,f(2π)=
f(π)=-
,f(3π)=-
,
…,f(nπ)=-(
)n-1.
由于当x∈[0,π)时,f′(x)•cos2x>f(x)•sin2x-f′(x),
则有f′(x)(1+cos2x)-f(x)sin2x>0,
即有2cosx(f′(x)cosx-f(x)sinx)>0,则2cosx•(f(x)cosx)′>0,
则有cosx>0,(f(x)cosx)′>0,f(x)cosx在(0,
)递增,
cosx<0,(f(x)cosx)′<0,f(x)cosx在(
,π)递减,
由于方程f(x)+knsecx=0在[0,+∞)上有n个解,
即有kn=-f(x)cosx在[0,+∞)上有n个解,
则k1=-f(0)cos0=2,k2=-f(π)cosπ=-1,k3=-f(2π)cos2π=
,k4=-f(3π)cos3π=-
,
…,kn=-f((n-1)π)cos(n-1)π,
则有k2n=(
)n-1,即有
=n•2n-1,
令S=1+2•2+3•22+…+n•2n-1,则2S=1•2+2•22+3•23+…+n•2n,
两式相减得,-S=1+2+22+23+…+2n-1-n•2n=
-n•2n
则S=(n-1)•2n+1.
故选A.
| 1 |
| 2 |
则f(π)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
…,f(nπ)=-(
| 1 |
| 2 |
由于当x∈[0,π)时,f′(x)•cos2x>f(x)•sin2x-f′(x),
则有f′(x)(1+cos2x)-f(x)sin2x>0,
即有2cosx(f′(x)cosx-f(x)sinx)>0,则2cosx•(f(x)cosx)′>0,
则有cosx>0,(f(x)cosx)′>0,f(x)cosx在(0,
| π |
| 2 |
cosx<0,(f(x)cosx)′<0,f(x)cosx在(
| π |
| 2 |
由于方程f(x)+knsecx=0在[0,+∞)上有n个解,
即有kn=-f(x)cosx在[0,+∞)上有n个解,
则k1=-f(0)cos0=2,k2=-f(π)cosπ=-1,k3=-f(2π)cos2π=
| 1 |
| 2 |
| 1 |
| 4 |
…,kn=-f((n-1)π)cos(n-1)π,
则有k2n=(
| 1 |
| 2 |
| n |
| k2n |
令S=1+2•2+3•22+…+n•2n-1,则2S=1•2+2•22+3•23+…+n•2n,
两式相减得,-S=1+2+22+23+…+2n-1-n•2n=
| 1-2n |
| 1-2 |
则S=(n-1)•2n+1.
故选A.
点评:本题考查导数的运用:求单调区间和极值,考查函数的零点问题,考查等比数列的通项和求和公式,考查错位相减法求数列的和,考查运算能力,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知集合A={x|x2-2x-3<0},B={y|1≤y≤4},则下列结论正确的是( )
| A、A∩B=∅ |
| B、(∁UA)∪B=(-1,+∞) |
| C、A∩B=(1,4] |
| D、(∁UA)∩B=[3,4] |
某保卫科安排了三名保安负责单位国庆7天(1-7号)长假的安全保卫工作,其中甲值班3天,乙和丙均值班2天,因为有事,甲不能值2号的班,乙不能值7号的班,则不同的值班表有( )
| A、46种 | B、48种 |
| C、90种 | D、144种 |
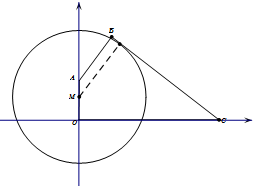 已知四边形OABC中,OA⊥OC,AB⊥BC,且OA=6,OC=17,tan∠BCO=
已知四边形OABC中,OA⊥OC,AB⊥BC,且OA=6,OC=17,tan∠BCO= 如图是一个几何体的三视图(单位:cm),计算这个几何体的体积与表面积.
如图是一个几何体的三视图(单位:cm),计算这个几何体的体积与表面积.