题目内容
当x∈[0,1]时,求函数f(x)=x2+(1-2a)x+a2的最小值g(a)的表达式.
考点:二次函数的性质
专题:函数的性质及应用
分析:先求出二次函数的对称轴,然后对对称轴的位置进行分类讨论,根据二次函数的单调性求得g(a)的表达式.
解答:
解:依题意知函数f(x)的对称轴方程为x=
,
当0≤
≤1时,即
≤a≤
时,g(a)=f(x)min=f(
)=
,
当
>1时,即a>
时,函数f(x)在[0,1]上单调减,g(a)=f(1)=a2-2a+2
当
<0时,即a<
时,函数f(x)在[0,1]上单调增,g(a)=f(0)=a2,
∴g(a)=
.
| 2a-1 |
| 2 |
当0≤
| 2a-1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2a-1 |
| 2 |
| 4a-1 |
| 4 |
当
| 2a-1 |
| 2 |
| 3 |
| 2 |
当
| 2a-1 |
| 2 |
| 1 |
| 2 |
∴g(a)=
|
点评:本题主要考查了二次函数的性质.运用了分类讨论的思想和数形结合的思想.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
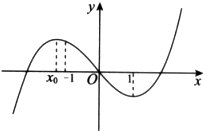 函数f(x)=ax3-bx2+cx的图象如图所示,且f(x)在x=x0与x=1处取得极值,给出下列判断:
函数f(x)=ax3-bx2+cx的图象如图所示,且f(x)在x=x0与x=1处取得极值,给出下列判断:①c>0;
②f(1)+f(-1)>0;
③函数y=f′(x)在区间(0,+∞)上是增函数.
其中正确的判断是( )
| A、①③ | B、② | C、②③ | D、①② |
 如图为正方体表面的一种展开图,则图中的四条线段AB,CD,EF,GH在原正方体中互为异面的对数为( )
如图为正方体表面的一种展开图,则图中的四条线段AB,CD,EF,GH在原正方体中互为异面的对数为( )| A、1 | B、2 | C、3 | D、4 |