题目内容
设a,b,c∈(-∞,0),则a+
,b+
,c+
( )
| 4 |
| b |
| 4 |
| c |
| 4 |
| a |
| A、都不大于-4 |
| B、都不小于-4 |
| C、至少有一个不大于-4 |
| D、至少有一个不小于-4 |
考点:反证法与放缩法
专题:证明题,反证法
分析:假设a+
,b+
,c+
都小于或等于-4,三式相加,得a+
+b+
+c+
≤-12,再结合基本不等式,即可得出结论.
| 4 |
| b |
| 4 |
| c |
| 4 |
| a |
| 4 |
| b |
| 4 |
| c |
| 4 |
| a |
解答:
解:假设a+
,b+
,c+
都小于或等于-4,
即a+
≤-4,b+
≤-4,c+
≤-4,
将三式相加,得a+
+b+
+c+
≤-12,
又因为a+
≤-4,b+
≤-4,c+
≤-4,
三式相加,得a+
+b+
+c+
≤-12,
所以a+
+b+
+c+
≤-12成立.
故选C.
| 4 |
| b |
| 4 |
| c |
| 4 |
| a |
即a+
| 4 |
| b |
| 4 |
| c |
| 4 |
| a |
将三式相加,得a+
| 4 |
| b |
| 4 |
| c |
| 4 |
| a |
又因为a+
| 4 |
| a |
| 4 |
| b |
| 4 |
| c |
三式相加,得a+
| 4 |
| b |
| 4 |
| c |
| 4 |
| a |
所以a+
| 4 |
| b |
| 4 |
| c |
| 4 |
| a |
故选C.
点评:本题考查反证法、不等式的性质和应用,解题时要注意均值不等式的合理运用.

练习册系列答案
相关题目
x=2是x2-4x+4=0的( )
| A、充分条件 |
| B、必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在△ABC中,“cosA=cosB”是“sinA=sinB”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
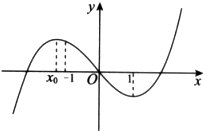 函数f(x)=ax3-bx2+cx的图象如图所示,且f(x)在x=x0与x=1处取得极值,给出下列判断:
函数f(x)=ax3-bx2+cx的图象如图所示,且f(x)在x=x0与x=1处取得极值,给出下列判断:①c>0;
②f(1)+f(-1)>0;
③函数y=f′(x)在区间(0,+∞)上是增函数.
其中正确的判断是( )
| A、①③ | B、② | C、②③ | D、①② |
计算定积分
xdx=( )
| ∫ | 2 0 |
| A、2 | B、1 | C、4 | D、-2 |
命题“对任意实数x,都有x>1”的否定是( )
| A、对任意实数x,都有x<1 |
| B、不存在实数x,使x≤1 |
| C、对任意实数x,都有x≤1 |
| D、存在实数x,使x≤1 |
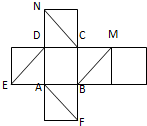 如图是正方体的平面展开图,在这个正方体中;
如图是正方体的平面展开图,在这个正方体中;(1)CN与AF平行;
(2)CN与BE是异面直线;
(3)CN与BM成60°;
(4)DE与BM垂直.
以上四个命题中,正确命题的序号是( )
| A、(1)(2)(3) |
| B、(2)(4) |
| C、(3)(4) |
| D、(3) |
