题目内容
已知θ是钝角三角形中的最小角，则sin（θ+
）的取值范围是（ ）
| π |
| 3 |
A、（
| ||||
B、[
| ||||
C、（
| ||||
D、[
|
考点：两角和与差的正弦函数
专题：三角函数的图像与性质
分析：由三角形的知识可得θ的范围，进而由三角函数的性质可得．
解答：
解：∵θ是钝角三角形中的最小角，∴0＜θ＜
，
∴
＜θ+
＜
，∴
＜sin（θ+
）≤1
∴sin（θ+
）的取值范围是（
，1]
故选：A
| π |
| 3 |
∴
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| ||
| 2 |
| π |
| 3 |
∴sin（θ+
| π |
| 3 |
| ||
| 2 |
故选：A
点评：本题考查三角函数的取值范围，得出θ的范围是解决问题的关键，属基础题．
练习册系列答案
相关题目
“a=1”是“函数f（x）=（x-1）2在区间[a，+∞）上为增函数”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
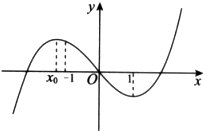函数f（x）=ax3-bx2+cx的图象如图所示，且f（x）在x=x0与x=1处取得极值，给出下列判断：①c＞0；
②f（1）+f（-1）＞0；
③函数y=f′（x）在区间（0，+∞）上是增函数．
其中正确的判断是（ ）
| A、①③ | B、② | C、②③ | D、①② |
命题“对任意实数x，都有x＞1”的否定是（ ）
| A、对任意实数x，都有x＜1 |
| B、不存在实数x，使x≤1 |
| C、对任意实数x，都有x≤1 |
| D、存在实数x，使x≤1 |
已知x，y满足约束条件
，则目标函数z=2x+y的最大值是（ ）
|
A、
| ||
B、2
| ||
C、
| ||
D、2
|
如图为正方体表面的一种展开图，则图中的四条线段AB，CD，EF，GH在原正方体中互为异面的对数为（ ）| A、1 | B、2 | C、3 | D、4 |