题目内容
已知曲线C的参数方程
（t为参数），C在点（1，1）处的切线为l，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，则l的极坐标方程为（ ）
|
A、ρ=
| ||||
B、ρsin（θ+
| ||||
C、ρsin（θ+
| ||||
D、ρ=sin（θ+
|
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：把参数方程消去参数化为直角坐标方程，再根据x=ρcosθ，y=ρsinθ，把直角坐标方程化为极坐标方程．
解答：
解：把曲线C的参数方程
（t为参数），消去参数化为普通方程为 x2+y2=2，
曲线C在点（1，1）处的切线为l：x+y=2，化为极坐标方程为 ρcosθ+ρsinθ=2，
即 ρsin（θ+
）=
，
故选：B．
|
曲线C在点（1，1）处的切线为l：x+y=2，化为极坐标方程为 ρcosθ+ρsinθ=2，
即 ρsin（θ+
| π |
| 4 |
| 2 |
故选：B．
点评：本题主要考查把参数方程化为直角坐标方程，把直角坐标方程化为极坐标方程的方法，属于基础题．
练习册系列答案
相关题目
已知在△ABC中，D是BC边上的中点，且AD=AC，DE⊥BC，DE与AB相交于点E，EC与AD相交于点F，S△FCD=5，BC=10，则DE=（ ）“a=1”是“函数f（x）=（x-1）2在区间[a，+∞）上为增函数”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
如果用反证法证明“数列{an}的各项均小于2”，那么应假设（ ）
| A、数列{an}的各项均大于2 |
| B、数列{an}的各项均大于或等于2 |
| C、数列{an}中存在一项ak，ak＞2 |
| D、数列{an}中存在一项ak，ak≥2 |
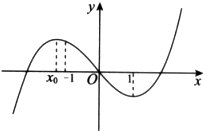函数f（x）=ax3-bx2+cx的图象如图所示，且f（x）在x=x0与x=1处取得极值，给出下列判断：①c＞0；
②f（1）+f（-1）＞0；
③函数y=f′（x）在区间（0，+∞）上是增函数．
其中正确的判断是（ ）
| A、①③ | B、② | C、②③ | D、①② |
已知x，y满足约束条件
，则目标函数z=2x+y的最大值是（ ）
|
A、
| ||
B、2
| ||
C、
| ||
D、2
|