题目内容
已知圆O:x2+y2=4和圆C:x2+(y-4)2=1.
(Ⅰ)判断圆O和圆C的位置关系;
(Ⅱ)过圆C的圆心C作圆O的切线l,求切线l的方程;
(Ⅲ)过圆C的圆心C作动直线m交圆O于A,B两点.试问:在以AB为直径的所有圆中,是否存在这样的圆P,使得圆P经过点M(2,0)?若存在,求出圆P的方程;若不存在,请说明理由.
(Ⅰ)判断圆O和圆C的位置关系;
(Ⅱ)过圆C的圆心C作圆O的切线l,求切线l的方程;
(Ⅲ)过圆C的圆心C作动直线m交圆O于A,B两点.试问:在以AB为直径的所有圆中,是否存在这样的圆P,使得圆P经过点M(2,0)?若存在,求出圆P的方程;若不存在,请说明理由.
考点:圆与圆的位置关系及其判定,直线与圆锥曲线的综合问题
专题:直线与圆
分析:(Ⅰ)求出两圆的半径和圆心距,由此能判断两圆的位置关系.
(Ⅱ)设切线l的方程为:y=kx+4,由圆心O到直线l的距离等于半径,能求出切线l的方程.
(Ⅲ)当直线m的斜率不存在时,直线m经过圆O的圆心O,由此得到圆O是满足题意的圆;当直线m的斜率存在时,设直线m:y=kx+4,由
,消去y整理,得(1+k2)x2+8kx+12=0,由此求出存在以AB为直径的圆P满足题意.从而能求出在以AB为直径的所有圆中,存在圆P:5x2+5y2-16x-8y+12=0或x2+y2=4,使得圆P经过点M(2,0).
(Ⅱ)设切线l的方程为:y=kx+4,由圆心O到直线l的距离等于半径,能求出切线l的方程.
(Ⅲ)当直线m的斜率不存在时,直线m经过圆O的圆心O,由此得到圆O是满足题意的圆;当直线m的斜率存在时,设直线m:y=kx+4,由
|
解答:
解:(Ⅰ)因为圆O的圆心O(0,0),半径r1=2,圆C的圆心C(0,4),半径r2=1,
所以圆O和圆C的圆心距|OC|=|4-0|>r1+r2=3,
所以圆O与圆C相离.…(3分)
(Ⅱ)设切线l的方程为:y=kx+4,即kx-y+4=0,
所以O到l的距离d=
=2,解得k=±
.
所以切线l的方程为
x-y+4=0或
x+y-4=0…(7分)
(Ⅲ)ⅰ)当直线m的斜率不存在时,直线m经过圆O的圆心O,
此时直线m与圆O的交点为A(0,2),B(0,-2),
AB即为圆O的直径,而点M(2,0)在圆O上,
即圆O也是满足题意的圆…(8分)
ⅱ)当直线m的斜率存在时,设直线m:y=kx+4,
由
,消去y整理,得(1+k2)x2+8kx+12=0,
由△=64k2-48(1+k2)>0,得k>
或k<-
.
设A(x1,y1),B(x2,y2),
则有
…①…(9分)
由①得y1y2=(kx1+4)(kx2+4)=k2x1x2+4k(x1+x2)+16=
,…②y1+y2=kx1+4+kx2+4=k(x1+x2)+8=
,…③
若存在以AB为直径的圆P经过点M(2,0),则MA⊥MB,所以
•
=0,
因此(x1-2)(x2-2)+y1y2=0,
即x1x2-2(x1+x2)+4+y1y2=0,…(10分)
则
+
+4+
=0,所以16k+32=0,k=-2,满足题意.
此时以AB为直径的圆的方程为x2+y2-(x1+x2)x-(y1+y2)y+x1x2+y1y2=0,
即x2+y2-
x-
y+
=0,亦即5x2+5y2-16x-8y+12=0.…(12分)
综上,在以AB为直径的所有圆中,
存在圆P:5x2+5y2-16x-8y+12=0或x2+y2=4,使得圆P经过点M(2,0)…(14分)
所以圆O和圆C的圆心距|OC|=|4-0|>r1+r2=3,
所以圆O与圆C相离.…(3分)
(Ⅱ)设切线l的方程为:y=kx+4,即kx-y+4=0,
所以O到l的距离d=
| |0+0+4| | ||
|
| 3 |
所以切线l的方程为
| 3 |
| 3 |
(Ⅲ)ⅰ)当直线m的斜率不存在时,直线m经过圆O的圆心O,
此时直线m与圆O的交点为A(0,2),B(0,-2),
AB即为圆O的直径,而点M(2,0)在圆O上,
即圆O也是满足题意的圆…(8分)
ⅱ)当直线m的斜率存在时,设直线m:y=kx+4,
由
|
由△=64k2-48(1+k2)>0,得k>
| 3 |
| 3 |
设A(x1,y1),B(x2,y2),
则有
|
由①得y1y2=(kx1+4)(kx2+4)=k2x1x2+4k(x1+x2)+16=
| 16-4k2 |
| 1+k2 |
| 8 |
| 1+k2 |
若存在以AB为直径的圆P经过点M(2,0),则MA⊥MB,所以
| MA |
| MB |
因此(x1-2)(x2-2)+y1y2=0,
即x1x2-2(x1+x2)+4+y1y2=0,…(10分)
则
| 12 |
| 1+k2 |
| 16k |
| 1+k2 |
| 16-4k2 |
| 1+k2 |
此时以AB为直径的圆的方程为x2+y2-(x1+x2)x-(y1+y2)y+x1x2+y1y2=0,
即x2+y2-
| 16 |
| 5 |
| 8 |
| 5 |
| 12 |
| 5 |
综上,在以AB为直径的所有圆中,
存在圆P:5x2+5y2-16x-8y+12=0或x2+y2=4,使得圆P经过点M(2,0)…(14分)
点评:本题考查两圆位置关系的判断,考查圆的切线方程的求法,考查满足条件的圆是否存在的判断与求法,解题时要认真审题,注意两点间距离公式的合理运用.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
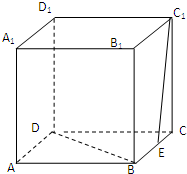 在正方体ABCD-A1B1C1D1中,E为BC的中点,求:
在正方体ABCD-A1B1C1D1中,E为BC的中点,求: