题目内容
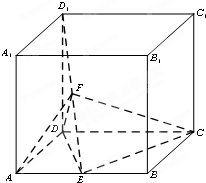 如图,四棱柱ABCD-A1B1C1D1中,DD1⊥底面ABCD.ABCD为平行四边形,∠DAB=60°,AB=2AD=2.DD1=3,E,F分别是AB与D1E的中点.
如图,四棱柱ABCD-A1B1C1D1中,DD1⊥底面ABCD.ABCD为平行四边形,∠DAB=60°,AB=2AD=2.DD1=3,E,F分别是AB与D1E的中点.(1)求证:CE⊥DF;
(2)求二面角A-EF-C的平面角的余弦值.
考点:与二面角有关的立体几何综合题,空间中直线与直线之间的位置关系
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明CE⊥平面DD1E,即可证明CE⊥DF;
(2)建立空间直角坐标系,求出平面AEF的一个法向量、平面CEF的一个法向量,利用向量的夹角公式,即可求二面角A-EF-C的平面角的余弦值.
(2)建立空间直角坐标系,求出平面AEF的一个法向量、平面CEF的一个法向量,利用向量的夹角公式,即可求二面角A-EF-C的平面角的余弦值.
解答:
 (1)证明:∵AD=AE,∠DAB=60°,∴△ADE为正△.
(1)证明:∵AD=AE,∠DAB=60°,∴△ADE为正△.
在△CDE中,由余弦定理可求CE=
,
又(
)2+12=22,
由勾股定理逆定理知CE⊥DE,
又DD1⊥平面ABCD,CE?平面ABCD,∴CE⊥DD1
∴CE⊥平面DD1E,
又DF?平面DD1E,∴CE⊥DF.
(2)解:以直线AB,AA1分别为x轴,z轴建立空间直角坐标系,
由题设A(0,0,0),E(1,0,0),D1(
,
,3),C(
,
,0)
可求平面AEF的一个法向量为
=(0,-2
,1),
平面CEF的一个法向量为
=(3,-3
,2)
∴平面角θ满足|cosθ|=
=
又θ为钝角,∴cosθ =-
.
 (1)证明:∵AD=AE,∠DAB=60°,∴△ADE为正△.
(1)证明:∵AD=AE,∠DAB=60°,∴△ADE为正△.在△CDE中,由余弦定理可求CE=
| 3 |
又(
| 3 |
由勾股定理逆定理知CE⊥DE,
又DD1⊥平面ABCD,CE?平面ABCD,∴CE⊥DD1
∴CE⊥平面DD1E,
又DF?平面DD1E,∴CE⊥DF.
(2)解:以直线AB,AA1分别为x轴,z轴建立空间直角坐标系,
由题设A(0,0,0),E(1,0,0),D1(
| 1 |
| 2 |
| ||
| 2 |
| 5 |
| 2 |
| ||
| 2 |
可求平面AEF的一个法向量为
| m |
| 3 |
平面CEF的一个法向量为
| n |
| 3 |
∴平面角θ满足|cosθ|=
|
| ||||
|
|
| ||
| 13 |
又θ为钝角,∴cosθ =-
| ||
| 13 |
点评:本题考查线面垂直、线线垂直、考查面面角,解题的关键是掌握线面垂直的判定,正确求出平面的法向量,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在△ABC中,AB=4,AC=1,∠BAC=60°.
如图,在△ABC中,AB=4,AC=1,∠BAC=60°. 在正方体ABCD-A1B1C1D1中,E为BC的中点,求:
在正方体ABCD-A1B1C1D1中,E为BC的中点,求: 如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点,求证:PO∥面D1BQ.
如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点,求证:PO∥面D1BQ.