题目内容
已知阶矩阵A=
,向量β=
(1)求阶矩阵A的特征值和特征向量;
(2)计算A2β
|
|
(1)求阶矩阵A的特征值和特征向量;
(2)计算A2β
考点:特征向量的定义,矩阵特征值的定义
专题:选作题,矩阵和变换
分析:(1)利用特征多项式,求特征值,进而可求特征向量;
(2)令β=m
+n
,则可得m=2,n=0,即可求出结论.
(2)令β=m
| α1 |
| α2 |
解答:
解:(1)矩阵A的特征多项式为f(λ)=(λ-3)(λ+1)
令f(λ)=0 解得A的特征值λ1=3,λ2=-1 …(6分)
当λ1=3 时,代入二元一次方程组
解得
,
∴特征值λ1=3 时的一个特征向量为
=
;…(8分
当λ2=-1时,同理可得特征值λ2=-1 时的一个特征向量为
=
…(10分)
(2)由(1)知
=
,
=
令β=m
+n
,则可得m=2,n=0 …(14分)
∴A2β=A2(2α1-0α2)=2(A2α1)=2×32
=
…(16分)
令f(λ)=0 解得A的特征值λ1=3,λ2=-1 …(6分)
当λ1=3 时,代入二元一次方程组
|
|
∴特征值λ1=3 时的一个特征向量为
| α1 |
|
当λ2=-1时,同理可得特征值λ2=-1 时的一个特征向量为
| α2 |
|
(2)由(1)知
| α1 |
|
| α2 |
|
令β=m
| α1 |
| α2 |
∴A2β=A2(2α1-0α2)=2(A2α1)=2×32
| α1 |
|
点评:本题考查特征值与特征向量,解题的关键是确定特征多项式,属于基础题.

练习册系列答案
相关题目
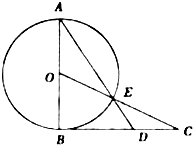 如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.
如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D. 如图,在△ABC中,AB=4,AC=1,∠BAC=60°.
如图,在△ABC中,AB=4,AC=1,∠BAC=60°.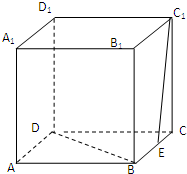 在正方体ABCD-A1B1C1D1中,E为BC的中点,求:
在正方体ABCD-A1B1C1D1中,E为BC的中点,求: 如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点,求证:PO∥面D1BQ.
如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点,求证:PO∥面D1BQ.