题目内容
已知数列{an}的前n项和为Sn,a1=1,且nSn+1-(n+1)Sn=
(n∈N+).
(1)求数列{an}的通项公式;
(2)记bn=
,证明:当n≥2时,b1+b2+b3+…+bn<
.
| n2+n |
| 2 |
(1)求数列{an}的通项公式;
(2)记bn=
| an+3 |
| 2an+1•an3 |
| 9 |
| 8 |
考点:等差数列的性质,数列递推式
专题:等差数列与等比数列
分析:(1)把给出的递推式两边同时除以n2+n,得到数列{
}为等差数列,由等差数列的通项公式求出Sn,然后利用an=Sn-Sn-1求数列{an}的通项公式;
(2)把数列{an}的通项公式代入bn=
,然后利用放缩法证明不等式.
| Sn |
| n |
(2)把数列{an}的通项公式代入bn=
| an+3 |
| 2an+1•an3 |
解答:
(1)解:由nSn+1-(n+1)Sn=
,得
-
=
.
∴数列{
}为等差数列.
∵a1=1,
∴
=
=1.
则
=1+
(n-1)=
.
∴Sn=
.
当n≥2时,an=Sn-Sn-1=
-
=n.
验证n=1时成立.
∴an=n;
(2)证明:bn=
=
.
∴b1+b2+b3+…+bn
=1+
+b3+b4+…+bn
<
+
+
+…+
=
+
=
-
<
.
| n2+n |
| 2 |
| Sn+1 |
| n+1 |
| Sn |
| n |
| 1 |
| 2 |
∴数列{
| Sn |
| n |
∵a1=1,
∴
| S1 |
| 1 |
| a1 |
| 1 |
则
| Sn |
| n |
| 1 |
| 2 |
| n+1 |
| 2 |
∴Sn=
| n2+n |
| 2 |
当n≥2时,an=Sn-Sn-1=
| n2+n |
| 2 |
| (n-1)2+n-1 |
| 2 |
验证n=1时成立.
∴an=n;
(2)证明:bn=
| an+3 |
| 2an+1•an3 |
| n+3 |
| 2n+1•n3 |
∴b1+b2+b3+…+bn
=1+
| 5 |
| 64 |
<
| 69 |
| 64 |
| 3 |
| 27 |
| 3 |
| 28 |
| 3 |
| 2n+4 |
| 69 |
| 64 |
| ||||
1-
|
=
| 72 |
| 64 |
| 3 |
| 2n+4 |
| 9 |
| 8 |
点评:本题考查了数列与不等式,考查了等差关系的确定,训练了利用放缩法证明数列不等式,是中高档题.

练习册系列答案
相关题目
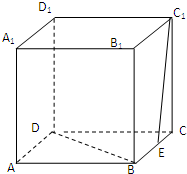 在正方体ABCD-A1B1C1D1中,E为BC的中点,求:
在正方体ABCD-A1B1C1D1中,E为BC的中点,求: 如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点,求证:PO∥面D1BQ.
如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点,求证:PO∥面D1BQ.