Question

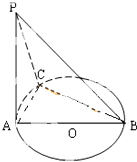如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆周上不同于A，B的任意一点，AC=BC=4，PA=4

2

，则二面角A-PB-C的大小的正弦值为（　　）

• A、

  2

  2

• B、

  2

  3

• C、

  6

  3

• D、

  3

  3

Answer 1

考点：二面角的平面角及求法

专题：计算题,空间角

分析：连接CO，过O在平面PAB上作OM⊥PB于M，连接CM，∠OMC是二面角A-PB-C的平面角，由此能求出二面角A-PB-C的大小的正弦值．

解答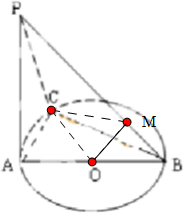： 解：如图，连接CO，∵AC=BC=4，PA=4

2

，∴AB=4

2

，∴AB⊥OC，
过O在平面PAB上作OM⊥PB于M，连接CM，由三垂线定理CM⊥PB，
∴∠OMC是二面角A-PB-C的平面角，
∵CO=2

2

，CM=2

3

，所以在Rt△ABC中sin∠OMC=

2 2

2 3

=

6

3

，
故选C．

点评：本题考查二面角A-PB-C的大小的正弦值，考查学生的计算能力，确定二面角A-PB-C的平面角是关键．