题目内容
已知集合M={1，2}，N={2a-1|a∈M}，则M∪N= ．
考点：并集及其运算
专题：集合
分析：利用并集的性质求解．
解答：
解：∵集合M={1，2}，N={2a-1|a∈M}={1，3}，
∴M∪N={1，2，3}．
故答案：{1，2，3}．
∴M∪N={1，2，3}．
故答案：{1，2，3}．
点评：本题考查并集的求法，解题时要认真审题，注意并集性质的合理运用．
练习册系列答案
相关题目
命题：“存在x0∈R，使得x02＜0”的否定为（ ）
| A、对任意的x∈R都有x2＜0 |
| B、存在x0∈R使得x02＞0 |
| C、存在x0∈R使得x02≥0 |
| D、对任意的x∈R都有x2≥0 |
已知α是第四象限的角，若cosα=
，则tanα=（ ）
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、
|
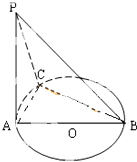如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆周上不同于A，B的任意一点，AC=BC=4，PA=4