题目内容
下列说法中，正确的是（ ）
| A、对任意x∈R，都有3x＞2x | ||
B、y=（
| ||
| C、若x∈R且x≠0，则log2x2=2log2x | ||
| D、函数y=x|x|是R上的增函数 |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：A中x=0时，不等式不成立；
B中由指数函数的性质判断y=(
)-x是R上的减函数；
C中x＜0时，2log2x无意义；
D中y=x|x|=
是R上的增函数．
B中由指数函数的性质判断y=(
| 3 |
C中x＜0时，2log2x无意义；
D中y=x|x|=
|
解答：
解：对于A，当x=0时，30=20=1，∴命题A错误；
对于B，y=(
)-x=(
)x是R上的减函数，∴命题B错误；
对于C，x＜0时，2log2x无意义，∴命题C错误；
对于D，y=x|x|=
，是R上的增函数，命题正确．
故选：D．
对于B，y=(
| 3 |
| 1 | ||
|
对于C，x＜0时，2log2x无意义，∴命题C错误；
对于D，y=x|x|=
|
故选：D．
点评：本题考查了函数的性质与应用问题，解题时应对每一个命题进行判断是否正确，是基础题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
如果函数f（x）=x2-2bx+2在区间[3，+∞）上是增函数，则b的取值范围为（ ）
| A、b=3 | B、b≥3 |
| C、b≤3 | D、b≠3 |
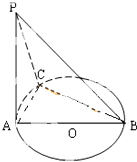如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆周上不同于A，B的任意一点，AC=BC=4，PA=4