题目内容
若函数f(x)=-x2-kx+1在(-∞,1]上是增函数,则实数k的取值范围是 .
考点:二次函数的性质
专题:函数的性质及应用
分析:先求出二次函数f(x)的对称轴,根据二次函数的单调性,由f(x)在(-∞,1]是增函数,得到限制k的不等式,解不等式即得k的取值范围.
解答:
解:函数f(x)的对称轴是:x=-
;
f(x)在(-∞,1]上是增函数,∴-
≥1,∴k≤-2;
∴实数k的取值范围是(-∞,-2].
故答案为:(-∞,-2].
| k |
| 2 |
f(x)在(-∞,1]上是增函数,∴-
| k |
| 2 |
∴实数k的取值范围是(-∞,-2].
故答案为:(-∞,-2].
点评:考查二次函数的单调性和对称轴的关系,也可画出抛物线及对称轴求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列集合中,只有一个子集的集合为( )
| A、{x|x2≤0} |
| B、{x|x3≤0} |
| C、{x|x2<0} |
| D、{x|x3<0} |
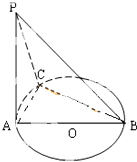 如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点,AC=BC=4,PA=4
如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点,AC=BC=4,PA=4