题目内容
已知函数f（x）对?a、b∈R都有f（a+b）=f（a）+f（b）-1，且当x＞0时，f（x）＞1．求证：f（x）在R上是增函数．
考点：函数单调性的判断与证明
专题：证明题,函数的性质及应用
分析：用定义法证明单调性一般可以分为五步，取值，作差，化简变形，判号，下结论．
解答：
证明：任取x1，x2∈R，且x1＜x2，则
∵对?a、b∈R都有f（a+b）=f（a）+f（b）-1，
∴f（x2）-f（x1）=f（x2-x1）-1，
又∵当x＞0时，f（x）＞1，
而x2-x1＞0，
∴f（x2）-f（x1）＞0，
即f（x）在R上是增函数．
∵对?a、b∈R都有f（a+b）=f（a）+f（b）-1，
∴f（x2）-f（x1）=f（x2-x1）-1，
又∵当x＞0时，f（x）＞1，
而x2-x1＞0，
∴f（x2）-f（x1）＞0，
即f（x）在R上是增函数．
点评：本题考查了函数单调性的证明，一般有两种方法，定义法，导数法．
练习册系列答案
相关题目
命题：“存在x0∈R，使得x02＜0”的否定为（ ）
| A、对任意的x∈R都有x2＜0 |
| B、存在x0∈R使得x02＞0 |
| C、存在x0∈R使得x02≥0 |
| D、对任意的x∈R都有x2≥0 |
已知α是第四象限的角，若cosα=
，则tanα=（ ）
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、
|
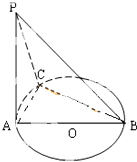如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆周上不同于A，B的任意一点，AC=BC=4，PA=4