题目内容
己知:f(x)=lnx-ax+1,
(1)当a=1时,求证:f(x)≤0
(2)当a∈R时,讨论函数的单调性.
(1)当a=1时,求证:f(x)≤0
(2)当a∈R时,讨论函数的单调性.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)当a=1时,f(x)=lnx-x+1,(x>0).f′(x)=
-1,分别令f′(x)>0,f′(x)<0,解出,即可得出单调性极值.
(2)f′(x)=
-a,(x>0).对a分类讨论:a≤0,a>0,利用导数研究函数的单调性.
| 1 |
| x |
(2)f′(x)=
| 1 |
| x |
解答:
(1)证明:当a=1时,f(x)=lnx-x+1,(x>0).
f′(x)=
-1=
,令f′(x)=0,解得x=1.
令f′(x)>0,解得0<x<1,此时函数f(x)单调递增;令f′(x)<0,解得1<x,此时函数f(x)单调递减.
∴当x=1时,函数f(x)取得极大值,即最大值,f(1)=0.
∴f(x)≤f(1)=0.
(2)解:f′(x)=
-a,(x>0).
当a≤0时,f′(x)>0,函数f(x)在(0,+∞)单调递增;
当a>0时,f′(x)=
,
令f′(x)>0,解得0<x<
;令f′(x)<0,解得x>
.
∴函数f(x)的单调递增区间为(0,
),单调递减为(
,+∞).
综上可得:当a≤0时,函数f(x)在(0,+∞)单调递增;
当a>0时,函数f(x)的单调递增区间为(0,
),单调递减为(
,+∞).
f′(x)=
| 1 |
| x |
| 1-x |
| x |
令f′(x)>0,解得0<x<1,此时函数f(x)单调递增;令f′(x)<0,解得1<x,此时函数f(x)单调递减.
∴当x=1时,函数f(x)取得极大值,即最大值,f(1)=0.
∴f(x)≤f(1)=0.
(2)解:f′(x)=
| 1 |
| x |
当a≤0时,f′(x)>0,函数f(x)在(0,+∞)单调递增;
当a>0时,f′(x)=
-a(x-
| ||
| x |
令f′(x)>0,解得0<x<
| 1 |
| a |
| 1 |
| a |
∴函数f(x)的单调递增区间为(0,
| 1 |
| a |
| 1 |
| a |
综上可得:当a≤0时,函数f(x)在(0,+∞)单调递增;
当a>0时,函数f(x)的单调递增区间为(0,
| 1 |
| a |
| 1 |
| a |
点评:本题考查了利用导数研究函数的单调性极值,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知α是第四象限的角,若cosα=
,则tanα=( )
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、
|
在等差数列{an}中,a5+a13=40,则a8+a9+a10=( )
| A、72 | B、60 | C、48 | D、36 |
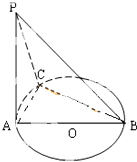 如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点,AC=BC=4,PA=4
如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B的任意一点,AC=BC=4,PA=4