Question

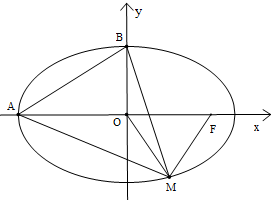M是椭圆T：

x2

a2

+

y2

b2

=1（a＞b＞0）上任意一点，F是椭圆T的右焦点，A为左顶点，B为上顶点，O为坐标原点，如下图所示，已知|MF|的最大值为3+

5

，最小值为3-

5

．
（1）求椭圆T的标准方程；
（2）求△ABM的面积的最大值S₀．若点N（x，y）满足x∈Z，y∈Z，称点N为格点．问椭圆T内部是否存在格点G，使得△ABG的面积S∈（6，S₀）？若存在，求出G的坐标；若不存在，请说明理由．（提示：点P（x₀，y₀）在椭圆T内部?

x02

a2

+

y02

b2

＜1）．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）由椭圆性质可知|MF|=

c

a

(

a2

c

-xM)=a-

c

a

xM，由已知条件得

a+c=3+ 5 a-c=3- 5

，由此能求出椭圆T的方程．
（2）由题知直线AB的方程为y=

2

3

x+2，设直线l：y=

2

3

x+m与椭圆T相切于x轴下方的点M₀，则△ABM₀的面积为△ABM的面积的最大值S₀．直线与椭圆联立求出直线AB与直线l距离为

2+2 2

1+ 4 9

=

3(2+2 2 )

13

，由此能求出（2，-1）为所求格点G．

解答： 解：（1）由椭圆性质可知|MF|=

c

a

(

a2

c

-xM)=a-

c

a

xM，
其中c＞0，c²=a²-b²，
因为x_M∈[-a，a]，故|MF|∈[a-c，a+c]
则

a+c=3+ 5 a-c=3- 5

，解之得

a=3 c= 5

…（4分）
故b²=a²-c²=4
椭圆T的方程为

x2

9

+

y2

4

=1…（5分）
（2）由题知直线AB的方程为y=

2

3

x+2，
设直线l：y=

2

3

x+m与椭圆T相切于x轴下方的点M₀，
则△ABM₀的面积为△ABM的面积的最大值S₀.

y= 2 3 x+m x2 9 + y2 4 =1

⇒

2

9

x2+

m

3

x+

m2

4

-1=0⇒△=

m2

9

-4•

2

9

(

m2

4

-1)=0⇒m=-2

2

此时，直线AB与直线l距离为

2+2 2

1+ 4 9

=

3(2+2 2 )

13

，
而|AB|=

13

S0=

1

2

•

13

•

3(2+2 2 )

13

=3(1+

2

)…（8分）
而S=

13

2

h，令6＜

13

2

h＜3(1+

2

)，则

12

13

＜h＜

3(1+ 2 )

13

设直线l1：y=

2

3

x+n到直线AB的距离为

12

13

，
则有

|n-2|

1+ 4 9

=

12

13

，解得n=-2或6，
注意到l₁与直线AB平行且l₁需与椭圆T应有公共点，
故只需考虑n=-2的情形．
直线y=

2

3

x-2经过椭圆T的下顶点B₀（0，-2）与右顶点A₀，
则线段A₀B₀上任意一点G₀与A、B组成的三角形的面积为6．…（10分）
根据题意若存在满足题意的格点G，则G必在直线A₀B₀与l之间．
而在椭圆内部位于四象限的格点为（1，-1），（2，-1）
因为-1＞

2

3

•1-2，故（1，-1）在直线A₀B₀上方，不符题意
而-1＜

2

3

•2-2，则点（2，-1）在直线A₀B₀下方，
且

22

9

+

(-1)2

4

=

25

36

＜1，点在椭圆内部，
所以（2，-1）为所求格点G．…（12分）

点评：本题考查椭圆方程的求法，考查满足条件的格点坐标是否存在的判断与求法，解题时要认真审题，注意函数与方程思想的合理运用．