题目内容
直线l过点M（1，1），与椭圆
+
=1相交于A、B两点，若AB的中点为M，试求：
（1）直线l的方程．
（2）求弦长AB．
| x2 |
| 4 |
| y2 |
| 3 |
（1）直线l的方程．
（2）求弦长AB．
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：（1）由于A，B两点是直线与椭圆的交点，故他们应满足椭圆方程，设出它们的坐标，然后根据它们的中点为M，可将坐标间的关系转化为求直线l的斜率，然后再由点斜式求出直线方程；
（2）3x+4y-7=0与椭圆
+
=1联立，利用韦达定理，结合弦长公式，可求弦长AB．
（2）3x+4y-7=0与椭圆
| x2 |
| 4 |
| y2 |
| 3 |
解答：
解：（1）设A（x1，y1）、B（x2，y2），
则
+
=1，①
+
=1②
①-②，得
+
=0．
又∵M为AB中点，
∴x1+x2=2，y1+y2=2．
∴直线l的斜率为-
．
∴直线l的方程为y-1=-
（x-1），即3x+4y-7=0．
（2）3x+4y-7=0与椭圆
+
=1联立可得21x2-42x+1=0，
设A（x1，y1），B（x2，y2），则x1+x2=2，x1x2=
，
∴|AB|=
•
=
．
则
| x12 |
| 4 |
| y12 |
| 3 |
| x22 |
| 4 |
| y22 |
| 3 |
①-②，得
| (x1-x2)(x1+x2) |
| 4 |
| (y1-y2)(y1+y2) |
| 3 |
又∵M为AB中点，
∴x1+x2=2，y1+y2=2．
∴直线l的斜率为-
| 3 |
| 4 |
∴直线l的方程为y-1=-
| 3 |
| 4 |
（2）3x+4y-7=0与椭圆
| x2 |
| 4 |
| y2 |
| 3 |
设A（x1，y1），B（x2，y2），则x1+x2=2，x1x2=
| 1 |
| 21 |
∴|AB|=
1+
|
4-
|
| 5 |
| 21 |
| 105 |
点评：本题考查直线与椭圆的综合，考查弦中点问题，正确运用点差法解决中点弦问题是解题的关键，属于中档题．
练习册系列答案
相关题目
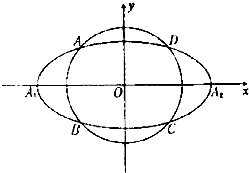如图，动圆C1：x2+y2=t2，1＜t＜3，与椭圆C2：
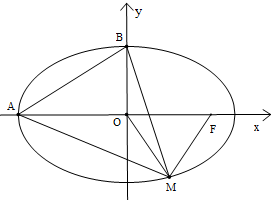M是椭圆T：
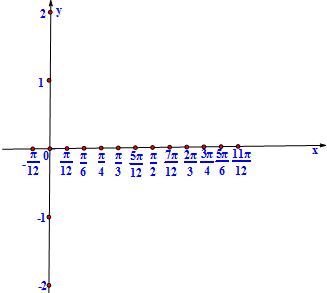已知函数f（x）=sin（2x-
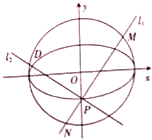已知椭圆E：