题目内容
已知△ABC中,a=10,B=60°,C=45°,求边c.
考点:余弦定理
专题:解三角形
分析:由条件利用三角形内角和公式求出A、利用两角和的正弦公式求出sinA,再由正弦定理求得c的值.
解答:
解:△ABC中,∵a=10,B=60°,C=45°,∴A=180°-B-C=75°,
∴sinA=sin(45°+30°)=sin45°cos30°+cos45°sin30°=
×
+
×
=
.
再由正弦定理可得,
=
,即
=
,解得c=10
-10.
∴sinA=sin(45°+30°)=sin45°cos30°+cos45°sin30°=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||||
| 4 |
再由正弦定理可得,
| a |
| sinA |
| c |
| sinC |
| 10 | ||||||
|
| c | ||||
|
| 3 |
点评:本题主要考查三角形内角和公式、两角和的正弦公式、正弦定理的应用,属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
某中学高一学生在数学研究性学习中,选择了“测量一个底部不可到达的建筑物的高度”的课题.设选择建筑物的顶点为A,假设A点离地面的高为AB.已知B,C,D三点依次在地面同一直线上,DC=a,从C,D两点测得A点的仰角分别为α,β(α>β),则A点离地面的高AB等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
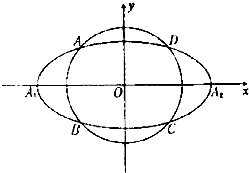 如图,动圆C1:x2+y2=t2,1<t<3,与椭圆C2:
如图,动圆C1:x2+y2=t2,1<t<3,与椭圆C2: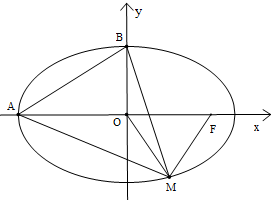 M是椭圆T:
M是椭圆T: 已知函数f(x)=sin(2x-
已知函数f(x)=sin(2x-