题目内容
现有长分别为1m、2m、3m的钢管各3根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取n根(假设各钢管被抽取的可能性是均等的,1≤n≤9),再将抽取的钢管相接焊成笔直的一根.
(Ⅰ)当n=3时,记事件A={抽取的3根钢管中恰有2根长度相等},求P(A);
(Ⅱ)当n=2时,若用ξ表示新焊成的钢管的长度(焊接误差不计),求ξ的分布列及E(ξ).
(Ⅰ)当n=3时,记事件A={抽取的3根钢管中恰有2根长度相等},求P(A);
(Ⅱ)当n=2时,若用ξ表示新焊成的钢管的长度(焊接误差不计),求ξ的分布列及E(ξ).
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:概率与统计
分析:(Ⅰ)由古黄概型概率计算公式给求出P(A).
(Ⅱ)ξ可能的取值为2,3,4,5,6,分别求出相应的概率,由此能求出ξ的分布列及E(ξ).
(Ⅱ)ξ可能的取值为2,3,4,5,6,分别求出相应的概率,由此能求出ξ的分布列及E(ξ).
解答:
解:(Ⅰ)事件A={抽取的3根钢管中恰有2根长度相等},
P(A)=
=
.…(4分)
(Ⅱ)ξ可能的取值为2,3,4,5,6,
P(ξ=2)=
=
,P(ξ=3)=
=
,
P(ξ=4)=
=
,P(ξ=5)=
=
,
P(ξ=6)=
=
…(9分)
∴ξ的分布列为:
…(10分)
Eξ=2×
+3×
+4×
+5×
+6×
=4.…(12分)
P(A)=
| ||||||
|
| 9 |
| 14 |
(Ⅱ)ξ可能的取值为2,3,4,5,6,
P(ξ=2)=
| ||
|
| 1 |
| 12 |
| ||||
|
| 1 |
| 4 |
P(ξ=4)=
| ||||||
|
| 1 |
| 3 |
| ||||
|
| 1 |
| 4 |
P(ξ=6)=
| ||
|
| 1 |
| 12 |
∴ξ的分布列为:
| ξ | 2 | 3 | 4 | 5 | 6 | ||||||||||
| P |
|
|
|
|
|
Eξ=2×
| 1 |
| 12 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
点评:本题考查概率的计算,考查离散型随机变量的概率分布列和数学期望的求法,是中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
如图是某产品加工为成品的流程图,从图中可以看出,即使是一件不合格产品,也必须经过几道工序( )


| A、6 | B、5 | C、4 | D、3 |
 如图,在山底测得山顶仰角∠CAB=45°,沿倾斜角为30°的斜坡走1000米至S点,又测得山顶仰角为75°,求山高BC.
如图,在山底测得山顶仰角∠CAB=45°,沿倾斜角为30°的斜坡走1000米至S点,又测得山顶仰角为75°,求山高BC.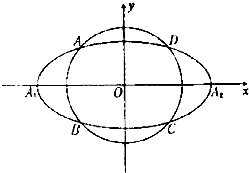 如图,动圆C1:x2+y2=t2,1<t<3,与椭圆C2:
如图,动圆C1:x2+y2=t2,1<t<3,与椭圆C2: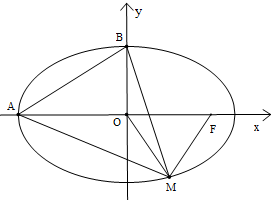 M是椭圆T:
M是椭圆T: