Question

若x，y满足约束条件

x+y≥1 -x+y≥1 2x-y≤2

，
（1）求目标函数z=

1

2

x-y+

1

2

的最值．
（2）若目标函数z=ax+2y仅在点（1，0）处取得最小值，求a的取值范围．
（3）求点P（x，y）到直线y=-x-2的距离的最大值．

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

分析：（1）作出可行域，利用目标函数的几何意义即可得到结论．
（2）若目标函数z=ax+2y仅在点（1，0）处取得最小值，判断目标函数的斜率关系，即可得到结论．
（3）根据点到直线的距离公式，利用数形结合即可求点P（x，y）到直线y=-x-2的距离的最大值．

解答： 解：（1）作出可行域如图，则直线x+y=1，x-y=-1，2x-y=2的交点分别为A（3，4），B（0，1），C（1，0），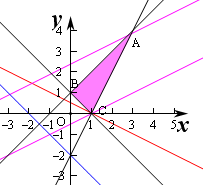
平移

1

2

x-y+

1

2

=0，由图象可知过A时，z取得最小值z=

1

2

×3-4+

1

2

=-2，
过C点取得最大值z=

1

2

+

1

2

=1．
∴z的最大值为1，最小值为-2．
（2）若目标函数z=ax+2y仅在点（1，0）处取得最小值，
则由图象可知-1＜-

a

2

＜2，
解得-4＜a＜2，
即a的取值范围（-4，2）．
（3）由图象可知，所求的最大值即是点A到直线x+y+2=0的距离，
则d=

|3+4+2|

1+1

=

9 2

2

．

点评：本题主要考查线性规划的应用，根据目标函数的几何意义是解决本题的关键．注意使用数形结合．