题目内容
设二次函数f(x)=-x2+2x.
(Ⅰ)求函数y=(
)f(x)的最小值;
(Ⅱ)问是否存在这样的正数m,n,当x∈[m,n]时,g(x)=f(x),且g(x)的值域为[
,
]?若存在,求出所有的m,n的值,若不存在,请说明理由.
(Ⅰ)求函数y=(
| 1 |
| 2 |
(Ⅱ)问是否存在这样的正数m,n,当x∈[m,n]时,g(x)=f(x),且g(x)的值域为[
| 1 |
| n |
| 1 |
| m |
考点:二次函数的性质
专题:函数的性质及应用
分析:(Ⅰ)先利用二次函数的性质求得函数f(x)的最小值,进而根据指数函数的单调性求得y的最小值.
(Ⅱ)先根据题意判断出1≤m<n,进而根据二次函数的单调性分别求得f(n)=
,f(m)=
求得n和m.
(Ⅱ)先根据题意判断出1≤m<n,进而根据二次函数的单调性分别求得f(n)=
| 1 |
| n |
| 1 |
| m |
解答:
解:(Ⅰ)f(x)=-(x-1)2+1≤1,
又y=(
)t,为减函数,因此,当x=1时y有最小值
.
(Ⅱ)g(x)=f(x)=2x-x2=-(x-1)2+1≤1,
又m>0,n>0,
∴
≤1,m≥1,即1≤m<n,f(x)为减函数,
于是
=g(n)=-n2+2n,即(n-1)(n2-n-1)=0,
∴
=g(m)=-m2+2m,即(m-1)(m2-m-1)=0,
∵1≤m<n,
∴m=1,n=
又y=(
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)g(x)=f(x)=2x-x2=-(x-1)2+1≤1,
又m>0,n>0,
∴
| 1 |
| m |
于是
| 1 |
| n |
∴
| 1 |
| m |
∵1≤m<n,
∴m=1,n=
1+
| ||
| 2 |
点评:本题主要考查了二次函数的性质.特别是对二次函数单调性的应用.

练习册系列答案
相关题目
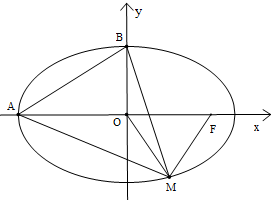 M是椭圆T:
M是椭圆T: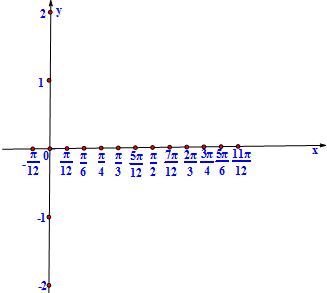 已知函数f(x)=sin(2x-
已知函数f(x)=sin(2x-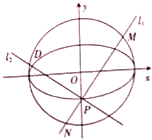 已知椭圆E:
已知椭圆E: