Question

16．设函数f'（x）是奇函数f（x）（x∈R）的导函数，f（-1）=0，当x＞0时，xf'（x）-f（x）＜0成立，则f（x）＞0的x的取值范围是（-∞，-1）∪（0，1）．

Answer 1

分析 由已知当x＞0时总有xf′（x）-f（x）＞0成立，可判断函数g（x）为增函数，由已知f（x）是定义在R上的奇函数，可证明g（x）为（-∞，0）∪（0，+∞）上的偶函数，根据函数g（x）在（0，+∞）上的单调性和奇偶性，而不等式f（x）＞0等价于xg（x）＞0，分类讨论即可求出．

解答 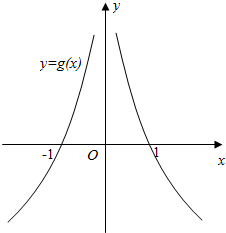解：设g（x）=$\frac{f（x）}{x}$，则g（x）的导数为：
g′（x）=$\frac{xf′（x）-f（x）}{{x}^{2}}$，
∵当x＞0时总有xf′（x）＜f（x）成立，
即当x＞0时，g′（x）恒小于0，
∴当x＞0时，函数g（x）=$\frac{f（x）}{x}$为减函数，
又∵g（-x）=g（x），
∴函数g（x）为定义域上的偶函数
又∵g（-1）=$\frac{f（-1）}{-1}$=0，
∴函数g（x）的大致图象如图所示：
数形结合可得，不等式f（x）＞0?x•g（x）＞0
?$\left\{\begin{array}{l}{x＞0}\\{g（x）＞0}\end{array}\right.$或$\left\{\begin{array}{l}{x＜0}\\{g（x）＜0}\end{array}\right.$，
?0＜x＜1或x＜-1．
∴f（x）＞0成立的x的取值范围是（-∞，-1）∪（0，1）．
故答案为：（-∞，-1）∪（0，1）

点评 本题考查了利用导数判断函数的单调性，并由函数的奇偶性和单调性解不等式的应用问题，是综合题目．