题目内容
8.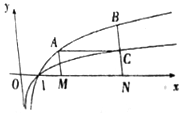 如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行.
如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行.(1)当a=2,b=4,c=3时,求实数m的值;
(2)当b=a2时,求$\frac{m}{b}$-$\frac{2c}{a}$的最小值;
(3)已知h(x)=ax,φ(x)=bx,若x1,x2为区间(a,b)任意两个变量,且x1<x2,求证:h(f(x2))<φ(f(x1))
分析 (1)根据A,C两点的纵坐标相等列方程即可解出m;
(2)据A,C两点的纵坐标相等得出a,b,c,m的关系,代入$\frac{m}{b}$-$\frac{2c}{a}$得出关于$\frac{c}{a}$的代数式,利用二次函数的性质得出最值;
(3)计算h(f(x2)),φ(f(x1)),利用指数函数,对数函数的单调性比较大小.
解答 解:(1)由题意得A(2,log32),B(4,log34),$C(4,log_m^{\;}4)$.
又AC与x轴平行,∴logm4=log32,
解得m=9.
(2)由题意得A(a,logca),B(b,logcb),$C(b,log_m^{\;}b)$.
∵AC与x轴平行,∴logmb=logca.
∵b=a2,∴m=c2,
∴$\frac{m}{b}-\frac{2c}{a}=\frac{c^2}{a^2}-\frac{2c}{a}={({\frac{c}{a}-1})^2}-1$.
∴$\frac{c}{a}=1$时,$\frac{m}{b}$-$\frac{2c}{a}$取得最小值-1.
(3)h(f(x2))=a${\;}^{lo{g}_{c}{x}_{2}}$,φ(x1)=b${\;}^{lo{g}_{c}{x}_{1}}$,
∵a<x1<x2<b,且c>1,∴logca<logcx1<logcx2<logcb.
又∵a>1,b>1,∴${a^{{{log}_c}{x_2}}}<{a^{{{log}_c}b}},{b^{{{log}_c}a}}<{b^{{{log}_c}{x_1}}}$.
又∵logcb•logca=logca•logcb,∴${log_c}{a^{{{log}_c}b}}={log_c}{b^{{{log}_c}a}}$.
∴${a^{{{log}_c}b}}={b^{{{log}_c}a}}$,∴${a^{{{log}_c}{x_2}}}<{b^{{{log}_c}{x_1}}}$.
即h[f(x2)]<φ(f(x1)).
点评 本题考查了对数计算,对数函数的性质和应用,属于中档题.

 口算能手系列答案
口算能手系列答案| A. | [-$\frac{π}{2}$,0] | B. | [-$\frac{π}{2}$,$\frac{π}{6}$) | C. | [-$\frac{π}{2}$,0) | D. | [-$\frac{π}{2}$,$\frac{π}{6}$] |
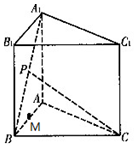 已知正三棱柱ABC-A1B1C的各条棱长都为a,P为A1B的中点,M为AB的中点,
已知正三棱柱ABC-A1B1C的各条棱长都为a,P为A1B的中点,M为AB的中点,