题目内容
17.函数y=ax-b(a>0且a≠1)的图象如图1所示,则函数y=cosax+b的图象可能是( )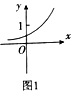
| A. | 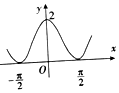 | B. | 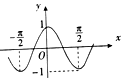 | ||
| C. |  | D. | 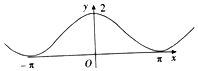 |
分析 先由函数y=ax-b(a>0且a≠1)的图象,可知a>1,b>0,再根据图象的平移即可判断函数的图象.
解答 解:由函数y=ax-b(a>0且a≠1)的图象,可知a>1,且0<a-b<1=a0,
∴-b<0,即b>0,
则函数y=cosax+b是由y=cosx的图象先纵坐标不变,横坐标拉伸为原来的$\frac{1}{a}$倍(即周期由2π,变为$\frac{2π}{a}$),再向上平移b个单位得到的,
故选:A.
点评 本题考查了指数函数和三角形函数的图象和变换,属于中档题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
5.如图是一个棱锥的三视图,则该棱锥的体积为( )


| A. | 12 | B. | 4 | C. | 6 | D. | 2 |
12.工人工资y(元)与劳动生产率x(千元)的相关关系的回归直线方程为$\widehat{y}$=50+80x,下列判断正确的是( )
| A. | 劳动生产率为1 000元时,工人工资为130元 | |
| B. | 劳动生产率提高1 000元时,工人工资平均提高80元 | |
| C. | 劳动生产率提高1 000元时,工人工资平均提高130元 | |
| D. | 当月工资为250元时,劳动生产率为2 000元 |
2.若实数x,y满足不等式组$\left\{\begin{array}{l}{x-y+2≥0}\\{x+2y-4≥0}\\{2x+y-5≤0}\end{array}\right.$且3(x-a)+2(y+1)的最大值为5,则a等于( )
| A. | -2 | B. | -1 | C. | 2 | D. | 1 |
6.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+x+a,x<0}\\{\frac{1}{x},x>0}\end{array}\right.$的图象上存在不同的两点 A,B,使得曲线y=f(x)在这两点处的切线重合,则实数a的取值范围是( )
| A. | ($\frac{1}{4}$,1) | B. | (2,+∞) | C. | $({-∞,-2})∪({\frac{1}{4},+∞})$ | D. | $({-∞,\frac{1}{4}})$ |
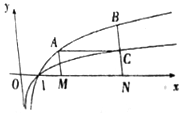 如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行.
如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行.