题目内容
20.若函数f(x)=(ex+ae-x)sinx为奇函数,则a=1.分析 由题意得(ex+ae-x)sinx=-sin(-x)(e-x+aex),从而化简求得.
解答 解:∵函数f(x)=(ex+ae-x)sinx为奇函数,
∴(ex+ae-x)sinx=-sin(-x)(e-x+aex),
∴ex+ae-x=e-x+aex,
故a=1.
故答案为:1
点评 本题考查了函数的奇偶性的判断与应用,属于基础题.

练习册系列答案
相关题目
11.函数f(x)=loga(2x-3)-4(a>0且a≠1)的图象恒过定点( )
| A. | (1,0) | B. | (1,-4) | C. | (2,0) | D. | (2,-4) |
15.计算sin46°•cos16°-cos314°•sin16°=( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{1}{2}$ |
5.如图是一个棱锥的三视图,则该棱锥的体积为( )


| A. | 12 | B. | 4 | C. | 6 | D. | 2 |
12.工人工资y(元)与劳动生产率x(千元)的相关关系的回归直线方程为$\widehat{y}$=50+80x,下列判断正确的是( )
| A. | 劳动生产率为1 000元时,工人工资为130元 | |
| B. | 劳动生产率提高1 000元时,工人工资平均提高80元 | |
| C. | 劳动生产率提高1 000元时,工人工资平均提高130元 | |
| D. | 当月工资为250元时,劳动生产率为2 000元 |
3.已知直线l:x-$\sqrt{3}$y+3=0与椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1交于A,B两点,过A,B分别作l的垂线与x轴交于C,D两点,则|CD|=( )
| A. | $\sqrt{3}$ | B. | $\frac{16}{13}$ | C. | $\frac{32}{13}$ | D. | $\frac{30}{13}$ |
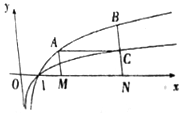 如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行.
如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行.