题目内容
18.已知各项均为正数的等比数列{an}的前三项为a,2,a+3,记前n项和为Sn.(1)设Sn=63,求a和n的值;
(2)令bn=(2n+1)an,求数列{bn}的前n项和Tn.
分析 (1)利用等比数列的中项性质和公比的定义,及其前n项和公式即可得出a,n;
(2)求得bn=(2n+1)an=(2n+1)•2n-1.利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(1)∵各项均为正数的等比数列{an}的前三项为a,2,a+3,
∴22=a(a+3),化为a2+3a-4=0,解得a=1或-4.
∵a>0,∴a=1.
∴a1=1,a2=2,公比q=$\frac{{a}_{2}}{{a}_{1}}$=2.
∴Sn=63=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$=$\frac{1-{2}^{n}}{1-2}$,解得n=6.
∴a=1,n=6.
(2)由(1)可得:an=2n-1.
bn=(2n+1)an=(2n+1)•2n-1.
∴数列{bn}的前n项和Tn=3•20+5•21+7•22+…+(2n+1)•2n-1,
∴2Tn=3•2+5•22+7•23+…+(2n+1)•2n,
∴-Tn=3+2(2+22+…+2n-1)-(2n+1)•2n
=3+2•$\frac{2(1-{2}^{n-1})}{1-2}$-(2n+1)•2n=(1-2n)•2n-1,
∴Tn=(2n-1)•2n+1.
点评 本题考查了等比数列的通项公式及其前n项和公式、数列的求和方法:“错位相减法”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.在一个个体数目为1002的总体中,要利用系统抽样抽取一个容量为50的样本,先用简单随机抽样删除两个个体,然后再从这1000个个体中抽50个个体,在这个过程中,每个个体被抽到的概率为( )
| A. | $\frac{1}{20}$ | |
| B. | $\frac{50}{1002}$ | |
| C. | $\frac{1}{1001}$ | |
| D. | 有两个个体与其它个体被抽到的概率不相等 |
13.某大学生从全校学生中随机选取100名统计他们的鞋码大小,得到如下数据:
以各性别各鞋码出现的频率为概率.
(1)从该校随机挑选一名学生,求他(她)的鞋码为奇数的概率;
(2)为了解该校学生考试作弊的情况,从该校随机挑选120名学生进行抽样调查.每位学生从装有除颜色外无差别的4个红球和6个白球的口袋中,随机摸出两个球,若同色,则如实回答其鞋码是否为奇数;若不同色,则如实回答是否曾在考试中作弊.这里的回答,是指在纸上写下“是”或“否”.若调查人员回收到32张“是”的小纸条,试估计该校学生在考试中曾有作弊行为的概率.
| 鞋码 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 合计 |
| 男生 | - | - | 3 | 6 | 8 | 11 | 12 | 6 | 7 | 2 | 55 |
| 女生 | 4 | 6 | 12 | 9 | 9 | 2 | 2 | - | - | 1 | 45 |
(1)从该校随机挑选一名学生,求他(她)的鞋码为奇数的概率;
(2)为了解该校学生考试作弊的情况,从该校随机挑选120名学生进行抽样调查.每位学生从装有除颜色外无差别的4个红球和6个白球的口袋中,随机摸出两个球,若同色,则如实回答其鞋码是否为奇数;若不同色,则如实回答是否曾在考试中作弊.这里的回答,是指在纸上写下“是”或“否”.若调查人员回收到32张“是”的小纸条,试估计该校学生在考试中曾有作弊行为的概率.
 在如图所示的几何体中,正方形ABEF所在的平面与正三角形ABC所在的平面互相垂直,CD∥BE,且BE=2CD,M是ED的中点.
在如图所示的几何体中,正方形ABEF所在的平面与正三角形ABC所在的平面互相垂直,CD∥BE,且BE=2CD,M是ED的中点.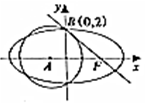 如图,点F为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点,圆A:(x-t)2+y2=$\frac{16}{3}$(t<0)与椭圆C的一个公共点为B(0,2),且直线FB与圆A相切于点B.
如图,点F为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右焦点,圆A:(x-t)2+y2=$\frac{16}{3}$(t<0)与椭圆C的一个公共点为B(0,2),且直线FB与圆A相切于点B.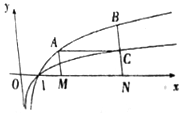 如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行.
如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行.