题目内容
19．若函数f（x）=（2x+2-x）ln（x+$\sqrt{a+{x}^{2}}$）为奇函数，则a=1．分析 根据定义域含原点的奇函数的图象过原点，求得a的值．
解答 解：∵函数f（x）=（2x+2-x）ln（x+$\sqrt{a+{x}^{2}}$） 为奇函数，且y=2x+2-x为偶函数，
∴y=ln（x+$\sqrt{a+{x}^{2}}$） 为奇函数，再根据它的图象过原点，可得0=ln$\sqrt{a}$，∴a=1，
故答案为：1．
点评 本题主要考查奇函数的性质，利用了定义域含原点的奇函数的图象过原点，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在如图所示的几何体中，正方形ABEF所在的平面与正三角形ABC所在的平面互相垂直，CD∥BE，且BE=2CD，M是ED的中点．
14．已知函数y=f（x）（x∈R）上任一点（x0，f（x0）），且在该点处的切线斜率为k=a（x0-1）（x0+2）2（a＜0），则该函数的单调递减区间为（ ）
| A． | [1，+∞） | B． | （-∞，1] | C． | （-2，1） | D． | [-2，+∞） |
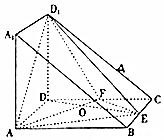将棱长为2的正方体沿对角A1BAD1截去一半得到如图所示的几何体，点E，F分别是BC，DC的中点，AF与DE相交于O点．
11．函数f（x）=loga（2x-3）-4（a＞0且a≠1）的图象恒过定点（ ）
| A． | （1，0） | B． | （1，-4） | C． | （2，0） | D． | （2，-4） |
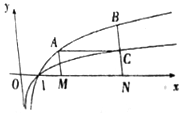如图，过函数f（x）=logcx（c＞1）的图象上的两点A，B作x轴的垂线，垂足分别为M（a，0），N（b，0）（b＞a＞1），线段BN与函数g（x）=logmx（m＞c＞1）的图象交于点C，且AC与x轴平行．