题目内容
16.函数y=$\sqrt{lo{g}_{5}(1-2sinx)}$,(-$\frac{π}{2}$≤x≤$\frac{π}{2}$)的定义域是( )| A. | [-$\frac{π}{2}$,0] | B. | [-$\frac{π}{2}$,$\frac{π}{6}$) | C. | [-$\frac{π}{2}$,0) | D. | [-$\frac{π}{2}$,$\frac{π}{6}$] |
分析 根据对数函数的性质列出不等式组,由对数函数的单调性、正弦函数的性质、条件求出函数的定义域.
解答 解:若函数$y=\sqrt{lo{g}_{5}(1-2sinx)}$有意义,
则$\left\{\begin{array}{l}{1-2sinx>0}\\{lo{g}_{5}^{(1-2sinx)}≥0}\end{array}\right.$,即1-2sinx≥1,
解得sinx≤0,
因为$-\frac{π}{2}≤x≤\frac{π}{2}$,所以$-\frac{π}{2}≤x≤0$,
即函数的定义域是$[-\frac{π}{2},0]$,
故选:A.
点评 本题考查函数的定义域及其求法,对数函数的单调性,以及正弦函数的性质,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
6.在一个个体数目为1002的总体中,要利用系统抽样抽取一个容量为50的样本,先用简单随机抽样删除两个个体,然后再从这1000个个体中抽50个个体,在这个过程中,每个个体被抽到的概率为( )
| A. | $\frac{1}{20}$ | |
| B. | $\frac{50}{1002}$ | |
| C. | $\frac{1}{1001}$ | |
| D. | 有两个个体与其它个体被抽到的概率不相等 |
11.函数f(x)=loga(2x-3)-4(a>0且a≠1)的图象恒过定点( )
| A. | (1,0) | B. | (1,-4) | C. | (2,0) | D. | (2,-4) |
1.设x>0,0<bx<ax<1,则正实数a,b的大小关系为( )
| A. | 1>a>b | B. | 1>b>a | C. | 1<a<b | D. | 1<b<a |
5.如图是一个棱锥的三视图,则该棱锥的体积为( )


| A. | 12 | B. | 4 | C. | 6 | D. | 2 |
6.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+x+a,x<0}\\{\frac{1}{x},x>0}\end{array}\right.$的图象上存在不同的两点 A,B,使得曲线y=f(x)在这两点处的切线重合,则实数a的取值范围是( )
| A. | ($\frac{1}{4}$,1) | B. | (2,+∞) | C. | $({-∞,-2})∪({\frac{1}{4},+∞})$ | D. | $({-∞,\frac{1}{4}})$ |
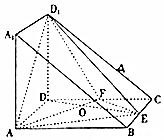 将棱长为2的正方体沿对角A1BAD1截去一半得到如图所示的几何体,点E,F分别是BC,DC的中点,AF与DE相交于O点.
将棱长为2的正方体沿对角A1BAD1截去一半得到如图所示的几何体,点E,F分别是BC,DC的中点,AF与DE相交于O点.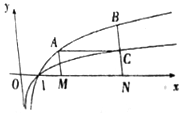 如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行.
如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行.