题目内容
13．已知命题p：“?x0∈R，x02-2x0+3≤0”的否定是“?x∈R，x2-2x+3＞0”，命题q：椭圆$\frac{{x}^{2}}{7}$+$\frac{{y}^{2}}{16}$=1的一个焦点坐标为（3，0），则下列命题中为真命题的是（ ）| A． | p∧q | B． | ￢p∧q | C． | ￢p∨q | D． | p∨q |
分析 先判定命题p、q的真假，再根据复合命题的真值表判定．
解答 解：命题p：“?x0∈R，x02-2x0+3≤0”的否定是“?x∈R，x2-2x+3＞0”，是真命题；
命题q：椭圆$\frac{{x}^{2}}{7}$+$\frac{{y}^{2}}{16}$=1的交点在y轴上，一个焦点坐标为（0，3），是假命题；
故p∧q为假命题；￢p∧q为假命题；￢p∨q为假命题；p∨q为真命题；
故选：D．
点评 本题考查了复合命题真假的判定，属于基础题．
练习册系列答案
相关题目
3．如图，在网格中粗线显示的为某几何体的三视图（正方形网格的边长为1），则该几何体的体积为（ ）
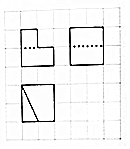
| A． | 5 | B． | 6 | C． | 6.5 | D． | 7 |
8．已知集合A={-1，0，1，3，4，5}，B={x|x2-4x+3≤0}，则A∩B=（ ）
| A． | {1} | B． | {3} | C． | {1，3} | D． | ∅ |
5．
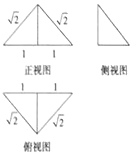一个四面体的三视图如图所示，则该四面体的外接球的表面积为（ ）
一个四面体的三视图如图所示，则该四面体的外接球的表面积为（ ）| A． | $\frac{4π}{3}$ | B． | 4π | C． | $\frac{2π}{3}$ | D． | 2π |
2．已知全集U=R，集合A={x|x＜-$\frac{1}{2}$或x＞1}，B={x|-1≤x≤2，x∈Z}，则图中阴影部分所表示的集合等于（ ）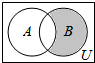
| A． | {-1，2} | B． | {-1，0} | C． | {0，1} | D． | {1，2} |
3．已知命题p：?x∈R，x2-2x-1≥0，则￢p是（ ）
| A． | ?x∈R，x2-2x-1≥0 | B． | ?x∈R，x2-2x-1＜0 | C． | ?x∈R，x2-2x-1＜0 | D． | ?x∈R，x2-2x-1≤0 |