题目内容
3．已知命题p：?x∈R，x2-2x-1≥0，则￢p是（ ）| A． | ?x∈R，x2-2x-1≥0 | B． | ?x∈R，x2-2x-1＜0 | C． | ?x∈R，x2-2x-1＜0 | D． | ?x∈R，x2-2x-1≤0 |
分析 本题中的命题是一个全称命题，其否定是特称命题，依据全称命题的否定书写形式：将量词“?”与“?”互换，结论同时否定，写出命题的否定即可．
解答 解：∵命题p：?x∈R，x2-2x-1≥0，
∴命题p的否定是“?x∈R，x2-2x-1＜0”
故答案为：?x∈R，x2-2x-1＜0，
故选：C．
点评 本题考查命题的否定，解题的关键是掌握并理解命题否定的书写方法规则，全称命题的否定是特称命题，特称命题的否定是全称命题，书写时注意量词的变化．
练习册系列答案
相关题目
13．已知命题p：“?x0∈R，x02-2x0+3≤0”的否定是“?x∈R，x2-2x+3＞0”，命题q：椭圆$\frac{{x}^{2}}{7}$+$\frac{{y}^{2}}{16}$=1的一个焦点坐标为（3，0），则下列命题中为真命题的是（ ）
| A． | p∧q | B． | ￢p∧q | C． | ￢p∨q | D． | p∨q |
11．△ABC中，B（-4，0），C（4，0），|AB|+|AC|=10，则顶点A的轨迹方程是（ ）
| A． | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1（x≠±3） | B． | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1（x≠±5） | ||
| C． | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1（x≠±3） | D． | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1（x≠±5） |
18．若?x0∈（0，+∞），不等式ax-lnx＜0成立，则a的取值范围是（ ）
| A． | （-∞，$\frac{1}{e}$） | B． | （-∞，0） | C． | （-∞，e） | D． | （-∞，1） |
8．
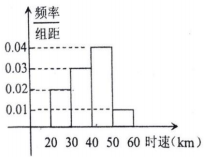太原市某时段100辆汽车通过祥云桥时，时速的频率分布直方图如图所示，则时速在[30，40]的汽车约有（ ）
太原市某时段100辆汽车通过祥云桥时，时速的频率分布直方图如图所示，则时速在[30，40]的汽车约有（ ）| A． | 30辆 | B． | 35辆 | C． | 40辆 | D． | 50辆 |