题目内容
5．
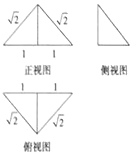一个四面体的三视图如图所示，则该四面体的外接球的表面积为（ ）| A． | $\frac{4π}{3}$ | B． | 4π | C． | $\frac{2π}{3}$ | D． | 2π |
分析 通过三视图，判断几何体的形状，利用三视图的数据，求出外接球的表面积，可得答案．
解答 解：由题意可知，几何体是三棱锥，
底面等腰直角三角形的底边长为2，底面三角形的高为：1，
棱锥的一条侧棱垂直底面的三角形的一个顶点，棱锥的高为：1．
其外接球的球心是底面斜边的中点，
故外接球的半径R=1，
∴外接球的表面积S=4πR2=4π，
故选：B．
点评 本题考查的知识点是由三视图求体积和表面积，球的表面积公式，根据已知，求出球的直径（半径）是解答的关键．
练习册系列答案
相关题目
16．已知角θ的始边与x轴的非负半轴重合，终边过点M（-3，4），则cos2θ的值为（ ）
| A． | $-\frac{7}{25}$ | B． | $\frac{7}{25}$ | C． | $-\frac{24}{25}$ | D． | $\frac{24}{25}$ |
13．已知命题p：“?x0∈R，x02-2x0+3≤0”的否定是“?x∈R，x2-2x+3＞0”，命题q：椭圆$\frac{{x}^{2}}{7}$+$\frac{{y}^{2}}{16}$=1的一个焦点坐标为（3，0），则下列命题中为真命题的是（ ）
| A． | p∧q | B． | ￢p∧q | C． | ￢p∨q | D． | p∨q |
20．《数学统综》有如下记载：“有凹线，取三数，小小大，存三角”．意思是说“在凹（或凸）函数（函数值为正）图象上取三个点，如果在这三点的纵坐标中两个较小数之和大于最大的数，则存在将这三点的纵坐标值作为三边长的三角形”．现已知凹函数f（x）=x2-2x+2，在$[\frac{1}{3}，{m^2}-m+2]$上任取三个不同的点（a，f（a）），（b，f（b）），（c，f（c）），均存在以f（a），f（b），f（c）为三边长的三角形，则实数m的取值范围为（ ）
| A． | [0，1] | B． | $[0，\frac{{\sqrt{2}}}{2}）$ | C． | $（0，\frac{{\sqrt{2}}}{2}]$ | D． | $[\frac{{\sqrt{2}}}{2}，\sqrt{2}]$ |