题目内容
3.如图,在网格中粗线显示的为某几何体的三视图(正方形网格的边长为1),则该几何体的体积为( )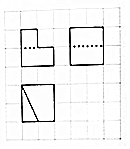
| A. | 5 | B. | 6 | C. | 6.5 | D. | 7 |
分析 由三视图可知,直观图是棱长为2的正方体,剪去一个底面是图形,高为1的四棱柱,即可求出几何体的体积.
解答 解:由三视图可知,直观图是棱长为2的正方体,剪去一个底面是图形,高为1的四棱柱,
所以几何体的体积为${2}^{3}-\frac{(1+2)×2}{2}×1$=5,
故选A.
点评 本题考查三视图,考查几何体体积的计算,确定直观图的形状是关键.

练习册系列答案
相关题目
13.点A(2,0)到直线l:y=x+2的距离为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
14.在平行六面体ABCD-A1B1C1D1中,AB=1,AD=1,AA1=2,∠BAD=90°,∠BAA1=∠DAA1=60°,则AC1的长为( )
| A. | $\sqrt{13}$ | B. | $\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 2+$\sqrt{3}$ |
11.设D表示不等式组$\left\{\begin{array}{l}{x≤1}&{\;}\\{y≤x}&{\;}\\{x+y≥1}&{\;}\end{array}\right.$所确定的平面区域,在D内存在无数个点落在y=a(x+2)上,则a的取值范围是( )
| A. | R | B. | ($\frac{1}{3}$,1) | C. | (0,$\frac{1}{3}$) | D. | (-∞,0]∪[$\frac{1}{3}$,+∞) |
18.已知集合A={x|y=$\sqrt{2x-{x}^{2}}$},集合B=Z,则A∩B=( )
| A. | {1} | B. | [0,2] | C. | (0,2) | D. | {0,1,2} |
8.已知sinα-sinβ=1-$\frac{\sqrt{3}}{2}$,cosα-cosβ=$\frac{1}{2}$,则cos(α-β)=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |