题目内容
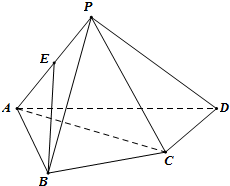 在四棱锥P-ABCD中,AB⊥BC,AC⊥CD,AB=BC,∠ADc=60°(即:底面是一幅三角板拼成)
在四棱锥P-ABCD中,AB⊥BC,AC⊥CD,AB=BC,∠ADc=60°(即:底面是一幅三角板拼成)(1)若PA中点为E,求证:BE∥面PCD
(2)若PA=PB=PC=3,PD与面PAC成30°角,求此四棱锥的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)设AC,AD的中点分别为G,F,由已知条件推导出BF∥面PCD,EF∥面PCD,从而面BEF∥面PCD,由此能证明BE∥面PCD.
(2)由已知得PG⊥面ABCD,CD⊥面PAC,从而∠CPD=30°,进而S△BCD=
+
,由此能求出四棱锥P-ABCD的体积.
(2)由已知得PG⊥面ABCD,CD⊥面PAC,从而∠CPD=30°,进而S△BCD=
| 9 |
| 4 |
3
| ||
| 2 |
解答:
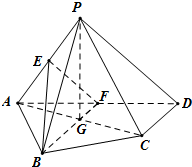 (1)证明:设AC,AD的中点分别为G,F,
(1)证明:设AC,AD的中点分别为G,F,
由已知得B,G,F三点共线,
∴BF∥CD,∵DC?平面PCD,BF?平面PCD,∴BF∥面PCD,
EF∥PD,∵PD?平面PCD,EF?平面PCD,∴EF∥面PCD,
又BF∩EF=F,∴面BEF∥面PCD,
∵BE?平面BEF,∴BE∥面PCD.(6分)
(2)解:∵PA=PB=PC,∴PG⊥面ABCD,
则有PG⊥CD,
又AC⊥CD,PG∩AC=G,∴CD⊥面PAC,
∴PC是PD在面PAC内的射影,
∵PD与面PAC成30°角,∴∠CPD=30°,(10分)
∵PA=PB=PC=3,∴CD=
,PG=
,AB=BC=
,
∴S△BCD=
+
,
∴V=
•(
+
)•
=
(2+
).(13分)
 (1)证明:设AC,AD的中点分别为G,F,
(1)证明:设AC,AD的中点分别为G,F,由已知得B,G,F三点共线,
∴BF∥CD,∵DC?平面PCD,BF?平面PCD,∴BF∥面PCD,
EF∥PD,∵PD?平面PCD,EF?平面PCD,∴EF∥面PCD,
又BF∩EF=F,∴面BEF∥面PCD,
∵BE?平面BEF,∴BE∥面PCD.(6分)
(2)解:∵PA=PB=PC,∴PG⊥面ABCD,
则有PG⊥CD,
又AC⊥CD,PG∩AC=G,∴CD⊥面PAC,
∴PC是PD在面PAC内的射影,
∵PD与面PAC成30°角,∴∠CPD=30°,(10分)
∵PA=PB=PC=3,∴CD=
| 3 |
3
| ||
| 2 |
3
| ||
| 2 |
∴S△BCD=
| 9 |
| 4 |
3
| ||
| 2 |
∴V=
| 1 |
| 3 |
| 9 |
| 4 |
3
| ||
| 2 |
3
| ||
| 2 |
| 9 |
| 8 |
| 3 |
点评:本题考查直线与平面平行的证明,考查四棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
已知某一随机变量X的分布列如下,则m的值为( )
| X | 4 | 7 | 9 |
| P | 0.5 | m | 0.4 |
| A、0.4 | B、0.3 |
| C、0.2 | D、0.1 |
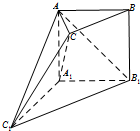 如图,在多面体ABC-A1B1C1中,侧面AA1B1B⊥底面A1B1C1,四边形AA1B1B是矩形,A1C1=A1B1,BC∥B1C1,B1C1=2BC.
如图,在多面体ABC-A1B1C1中,侧面AA1B1B⊥底面A1B1C1,四边形AA1B1B是矩形,A1C1=A1B1,BC∥B1C1,B1C1=2BC.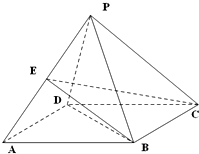 如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=