题目内容
已知
=2，求（sinθ+2）（cosθ+3）的值．
| cos2θ+4 |
| sinθ+1 |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：已知等式变形后，利用同角三角函数间基本关系化简，求出sinθ的值，进而求出cosθ的值，代入原式计算即可得到结果．
解答：
解：已知等式变形得：cos2θ+4=1-sin2θ+4=2sinθ+2，
整理得：sin2θ-2sinθ-3=0，即（sinθ-3）（sinθ+1）=0，
解得：sinθ=3（舍去）或sinθ=-1，
∵sin2θ+cos2θ=1，sinθ=-1，
∴cosθ=0，
则原式=3．
整理得：sin2θ-2sinθ-3=0，即（sinθ-3）（sinθ+1）=0，
解得：sinθ=3（舍去）或sinθ=-1，
∵sin2θ+cos2θ=1，sinθ=-1，
∴cosθ=0，
则原式=3．
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
幂函数f（x）的图象过点（3，
），则f（x）的解析式为（ ）
| 3 |
| A、f（x）=3x | ||
| B、f（x）=x3 | ||
C、f（x）=x
| ||
D、f（x）=（
|
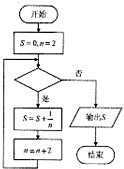阅读如图所示的程序框图，运行相应的程序，若输出的S为| 11 |
| 12 |
| A、n=6 | B、n＜6 |
| C、n≤6 | D、n≤8 |