题目内容
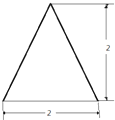 一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示该四棱锥侧面积和体积分别是( )
一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示该四棱锥侧面积和体积分别是( )A、4
| ||||
B、4
| ||||
C、4(
| ||||
| D、8,8 |
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:由已知得该四棱锥为正四棱锥,底面边长AB=2,高PO=2,由此能求出该四棱锥侧面积和体积.
解答:
解:∵四棱锥的侧棱长都相等,底面是正方形,
∴该四棱锥为正四棱锥,
其主视图为原图形中的△SEF,如图,
由该四棱锥的主视图可知四棱锥的底面边长AB=2,高PO=2,
则四棱锥的斜高PE=
=
.
∴该四棱锥侧面积S=4×
×2×
=4
,
体积V=
×2×2×2=
.
故选:B.

∴该四棱锥为正四棱锥,
其主视图为原图形中的△SEF,如图,
由该四棱锥的主视图可知四棱锥的底面边长AB=2,高PO=2,
则四棱锥的斜高PE=
| 22+12 |
| 5 |
∴该四棱锥侧面积S=4×
| 1 |
| 2 |
| 5 |
| 5 |
体积V=
| 1 |
| 3 |
| 8 |
| 3 |
故选:B.
点评:本题考查四棱锥侧面积和体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个正方体的对角线长为l,那么这个正方体的全面积为( )
A、2
| ||
| B、2l2 | ||
C、2
| ||
D、3
|
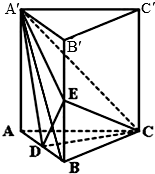 如图,直三棱柱ABC-A′B′C′中,AC=BC=5,AA′=AB=6,D、E分别为AB和BB′上的点,且
如图,直三棱柱ABC-A′B′C′中,AC=BC=5,AA′=AB=6,D、E分别为AB和BB′上的点,且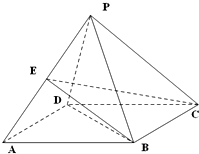 如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,已知PB=PD=2,PA=