题目内容
数列{an}定义如下:a1=1,且当n≥2时,an=
,若an=
,则正整数n=( )
|
| 19 |
| 11 |
| A、112 | B、114 |
| C、116 | D、118 |
考点:数列递推式
专题:等差数列与等比数列
分析:由已知条件分别求出数列的第112项、114项、116项和118项,由此能求出结果.
解答:
解:∵a1=1,且当n≥2时,an=
,
a2=1+1=2,a3=
=
,a7=
=
=
,
∴a112=a56+1=a28+2=a14+3=a7+4=
+4=
,
a114=a57+1=
+1=
+1=
+1=
+1=
,
a116=a58+1=a29+2=
+2=
+2=
+2=
,
a118=a59+1=
+1=
+1=
+1=
+1
=
+1=
+1=
.
∵an=
,∴正整数n=118.
故选:D.
|
a2=1+1=2,a3=
| 1 |
| a2 |
| 1 |
| 2 |
| 1 |
| a6 |
| 1 |
| a3+1 |
| 2 |
| 3 |
∴a112=a56+1=a28+2=a14+3=a7+4=
| 2 |
| 3 |
| 14 |
| 3 |
a114=a57+1=
| 1 |
| a56 |
| 1 |
| a28+1 |
| 1 |
| a14+2 |
| 1 |
| a7+3 |
| 20 |
| 11 |
a116=a58+1=a29+2=
| 1 |
| a28 |
| 1 |
| a14+1 |
| 1 |
| a7+2 |
| 19 |
| 8 |
a118=a59+1=
| 1 |
| a58 |
| 1 |
| a29+1 |
| 1 | ||
|
| 1 | ||
|
=
| 1 | ||
|
| 8 |
| 11 |
| 19 |
| 11 |
∵an=
| 19 |
| 11 |
故选:D.
点评:本题考查数列的项数的求法,是中档题,解题时要注意递推公式的合理运用.

练习册系列答案
相关题目
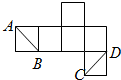
如图是正方体的平面展开图,则在这个正方体中AB与CD的位置关系为( )

| A、平行 |
| B、相交成60°角 |
| C、异面且垂直 |
| D、异面且成60°角 |
双曲线
-y2=1的焦点到渐近线的距离为( )
| x2 |
| m |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
△ABC中,sinA:sinB:sinC=4:7:8,则△ABC一定为( )
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
当实数x,y满足
时,1≤ax+y≤4恒成立,则实数a的取值范围是( )
|
A、[-
| ||||
B、[-
| ||||
C、[1,
| ||||
D、[
|
在(x-
)8的二项展开式中,常数项为( )
| 2 | |||
|
| A、1024 | B、1324 |
| C、1792 | D、-1080 |