题目内容
当实数x,y满足
时,1≤ax+y≤4恒成立,则实数a的取值范围是( )
|
A、[-
| ||||
B、[-
| ||||
C、[1,
| ||||
D、[
|
考点:简单线性规划
专题:不等式的解法及应用
分析:由约束条件作出可行域,再由1≤ax+y≤4恒成立,结合可行域内特殊点A,B,C的坐标满足不等式列不等式组,求解不等式组得实数a的取值范围.
解答:
解:由约束条件作可行域如图,
 联立
联立
,解得C(1,
).
联立
,解得B(2,1).
在x-y-1=0中取y=0得A(1,0).
要使1≤ax+y≤4恒成立,
则
,解得:1≤a≤
.
∴实数a的取值范围是[1,
].
故选:C
 联立
联立
|
| 3 |
| 2 |
联立
|
在x-y-1=0中取y=0得A(1,0).
要使1≤ax+y≤4恒成立,
则
|
| 3 |
| 2 |
∴实数a的取值范围是[1,
| 3 |
| 2 |
故选:C
点评:本题考查线性规划,考查了数形结合的解题思想方法,考查了数学转化思想方法,训练了不等式组得解法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数列{an}定义如下:a1=1,且当n≥2时,an=
,若an=
,则正整数n=( )
|
| 19 |
| 11 |
| A、112 | B、114 |
| C、116 | D、118 |
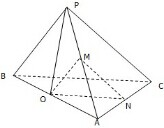 已知三棱锥P-ABC中,PA=PB=PC,BC⊥AC,M为PA中点,P在面ABC上的射影为O,O在AC上的射影为N,求证:平面OMN∥平面PBC.
已知三棱锥P-ABC中,PA=PB=PC,BC⊥AC,M为PA中点,P在面ABC上的射影为O,O在AC上的射影为N,求证:平面OMN∥平面PBC.