题目内容
△ABC中，sinA：sinB：sinC=4：7：8，则△ABC一定为（ ）
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
考点：三角形的形状判断,正弦定理,余弦定理
专题：解三角形
分析：根据正弦定理和余弦定理即可得到结论．
解答：
解：由正弦定理可得a：b：c=sinA：sinB：sinC=4：7：8，
设a=4x，b=7x，c=8x，x＞0，则c边最大，
由余弦定理可得cosC=
=
=
＞0，
则△ABC的最大角为锐角，
则△ABC是锐角三角形，
故选：A
设a=4x，b=7x，c=8x，x＞0，则c边最大，
由余弦定理可得cosC=
| a2+b2-c2 |
| 2ab |
| 16x2+49x2-64x2 |
| 2•4•7x2 |
| 1 |
| 56 |
则△ABC的最大角为锐角，
则△ABC是锐角三角形，
故选：A
点评：本题主要考查三角形形状的判断，根据正弦定理和余弦定理是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
数列{an}定义如下：a1=1，且当n≥2时，an=
，若an=
，则正整数n=（ ）
|
| 19 |
| 11 |
| A、112 | B、114 |
| C、116 | D、118 |
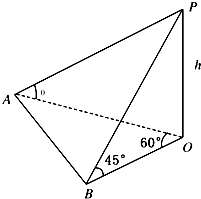地平面上一旗杆OP，为测得它的高度h，在地平面上取一基线AB，AB=30m，在A处测得旗杆顶P点的仰角为θ且tanθ=