题目内容
已知函数f(x)=ln(x-1)-k(x-1)+1(k∈R),
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若f(x)≤0恒成立,试确定实数k的取值范围;
(Ⅲ)证明:
+
+…+
<
(n∈N,n>1).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若f(x)≤0恒成立,试确定实数k的取值范围;
(Ⅲ)证明:
| ln2 |
| 3 |
| ln3 |
| 4 |
| lnn |
| n+1 |
| n(n-1) |
| 4 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ) 先求导,再分类讨论,根据导数即可得出函数的单调区间.
(Ⅱ)利用导数研究函数的单调性,求出函数的最大值,使最大值小于等于0,可求出k的取值范围;
(Ⅲ)由(1)可知,若k=1,当x∈(1,+∞)时有f(x)≤0,由此得到lnx<x-2(x>1),依次取x的值为2,3,…,n,累加后利用放缩法可证不等式成立.
(Ⅱ)利用导数研究函数的单调性,求出函数的最大值,使最大值小于等于0,可求出k的取值范围;
(Ⅲ)由(1)可知,若k=1,当x∈(1,+∞)时有f(x)≤0,由此得到lnx<x-2(x>1),依次取x的值为2,3,…,n,累加后利用放缩法可证不等式成立.
解答:
解:(Ⅰ)∵f(x)=ln(x-1)-k(x-1)+1,(x>1)
∴f′(x)=
-k,
当k≤0时,f′(x)>0恒成立,故函数在(1,+∞)为增函数,
当k>0时,令f′(x)=0,得x=
当f′(x)>0,即1<x<
时,函数为增函数,
当f′(x)<0,即x>
时,函数为减函数,
综上所述,当k≤0时,函数f(x)在(1,+∞)为增函数,
当k>0时,函数f(x)在(1,
)为增函数,在(
,+∞)为减函数.
(Ⅱ)由(Ⅰ)知,当k≤0时,f′(x)>0函数f(x)在定义域内单调递增,f(x)≤0不恒成立,
当k>0时,函数f(x)在(1,
)为增函数,在(
,+∞)为减函数.
当x=
时,f(x)取最大值,f(
)=ln
≤0
∴k≥1,
即实数k的取值范围为[1,+∞)
(Ⅲ)由(Ⅱ)知k=1时,f(x)≤0恒成立,即ln(x-1)<x-2
∴
<1-
,
取x=3,4,5…n,n+1累加得,
∵
=
=
<
=
∴
+
+…+
<
+
+
+…+
=
,(n∈N,n>1).
∴f′(x)=
| 1 |
| x-1 |
当k≤0时,f′(x)>0恒成立,故函数在(1,+∞)为增函数,
当k>0时,令f′(x)=0,得x=
| k+1 |
| k |
当f′(x)>0,即1<x<
| k+1 |
| k |
当f′(x)<0,即x>
| k+1 |
| k |
综上所述,当k≤0时,函数f(x)在(1,+∞)为增函数,
当k>0时,函数f(x)在(1,
| k+1 |
| k |
| k+1 |
| k |
(Ⅱ)由(Ⅰ)知,当k≤0时,f′(x)>0函数f(x)在定义域内单调递增,f(x)≤0不恒成立,
当k>0时,函数f(x)在(1,
| k+1 |
| k |
| k+1 |
| k |
当x=
| k+1 |
| k |
| k+1 |
| k |
| 1 |
| k |
∴k≥1,
即实数k的取值范围为[1,+∞)
(Ⅲ)由(Ⅱ)知k=1时,f(x)≤0恒成立,即ln(x-1)<x-2
∴
| ln(x-1) |
| x |
| 2 |
| x |
取x=3,4,5…n,n+1累加得,
∵
| ln |
| n+1 |
| 2lnn |
| 2(n+1) |
| lnn2 |
| 2(n+1) |
| n2-1 |
| 2(n+1) |
| n-1 |
| 2 |
∴
| ln2 |
| 3 |
| ln3 |
| 4 |
| lnn |
| n+1 |
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 2 |
| n-1 |
| 2 |
| n(n-1) |
| 4 |
点评:本题考查利用导数求函数的极值,函数的恒成立问题,不等式的证明,体现了分类讨论的数学思想,不等式的放缩,是解题的难点.

练习册系列答案
相关题目
数列{an}定义如下:a1=1,且当n≥2时,an=
,若an=
,则正整数n=( )
|
| 19 |
| 11 |
| A、112 | B、114 |
| C、116 | D、118 |
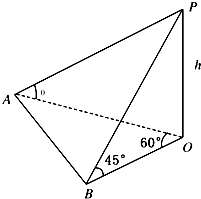 地平面上一旗杆OP,为测得它的高度h,在地平面上取一基线AB,AB=30m,在A处测得旗杆顶P点的仰角为θ且tanθ=
地平面上一旗杆OP,为测得它的高度h,在地平面上取一基线AB,AB=30m,在A处测得旗杆顶P点的仰角为θ且tanθ=| 1 |
| 2 |
在同一直角坐标系中,函数f(x)=logax(a>0,a≠1)与函数g(x)=ax(a>0,a≠1)的图象可能是( )
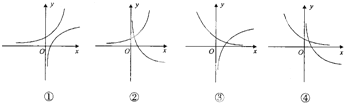

| A、①② | B、①③ | C、①④ | D、②④ |