题目内容
我们知道:圆的任意一弦(非直径)的中点和圆心连线与该弦垂直;那么,若椭圆b2x2+a2y2=a2b2的一弦(非过原点的弦)的中点与原点连线及弦所在直线的斜率均存在,你能得到什么结论?请予以证明.
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设点作差,利用中点坐标公式,即可得出结论.
解答:
解:设弦的两个端点分别为A(x1,y1),B(x2,y2),
设弦AB的中点为M(x0,y0),这样2x0=x1+x2和2y0=y1+y2,
所以b2x12+a2y12=a2b2 ①,b2x22+a2y22=a2b2 ②,
作差,整理可得2b2x0+2a2y0 •kAB =0,
所以kOM kAB =-
,得证.
设弦AB的中点为M(x0,y0),这样2x0=x1+x2和2y0=y1+y2,
所以b2x12+a2y12=a2b2 ①,b2x22+a2y22=a2b2 ②,
作差,整理可得2b2x0+2a2y0 •kAB =0,
所以kOM kAB =-
| b2 |
| a2 |
点评:本题考查椭圆的简单性质,考查点差法,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
数列{an}定义如下:a1=1,且当n≥2时,an=
,若an=
,则正整数n=( )
|
| 19 |
| 11 |
| A、112 | B、114 |
| C、116 | D、118 |
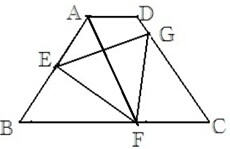 如图,梯形ABCD,AD∥BC,AB=CD=6,AD=2,BC=8,∠B=60°,点E在AB上,点F在BC上,
如图,梯形ABCD,AD∥BC,AB=CD=6,AD=2,BC=8,∠B=60°,点E在AB上,点F在BC上,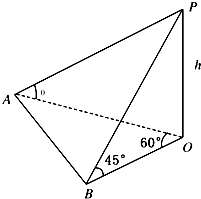 地平面上一旗杆OP,为测得它的高度h,在地平面上取一基线AB,AB=30m,在A处测得旗杆顶P点的仰角为θ且tanθ=
地平面上一旗杆OP,为测得它的高度h,在地平面上取一基线AB,AB=30m,在A处测得旗杆顶P点的仰角为θ且tanθ=