题目内容
已知函数f (x)=xlnx(x∈(0,+∞)).
(Ⅰ)求f (x)的单调区间;
(Ⅱ)若函数g(x)=2f (x)-blnx+x在x∈[1,+∞)上存在零点,求实数b的取值范围;
(Ⅲ)任取两个不等的正数x1、x2,且x1<x2,若存在x0>0使f'(x0)=
成立,求证:x0>x1.
(Ⅰ)求f (x)的单调区间;
(Ⅱ)若函数g(x)=2f (x)-blnx+x在x∈[1,+∞)上存在零点,求实数b的取值范围;
(Ⅲ)任取两个不等的正数x1、x2,且x1<x2,若存在x0>0使f'(x0)=
| f(x2)-f(x1) |
| x2-x1 |
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(Ⅰ)求导数,利用导数的正负求f (x)的单调区间;
(Ⅱ)若函数g(x)=2f (x)-blnx+x在x∈[1,+∞)上存在零点,方程2xlnx-blnx+x=0在x∈[1,+∞)上有实数解,即方程b=2x+
在x∈(1,+∞)上有实数解,即可求实数b的取值范围;
(Ⅲ)求出f′(x0),代入f′(x0)=
把lnx0用lnx1,lnx2表示,再用分析法进行证明.
(Ⅱ)若函数g(x)=2f (x)-blnx+x在x∈[1,+∞)上存在零点,方程2xlnx-blnx+x=0在x∈[1,+∞)上有实数解,即方程b=2x+
| x |
| lnx |
(Ⅲ)求出f′(x0),代入f′(x0)=
| f(x2)-f(x1) |
| x2-x1 |
解答:
解:(Ⅰ)∵f (x)=xlnx,∴f′(x)=lnx+1,
由lnx+1>0,即x>
时f′(x)>0,所以f(x)在区间(
,+∞)上单调递增,
由lnx+1<0,即0<x<
时f′(x)<0,所以f(x)在区间(0,
)上单调递减,
∴函数f(x)的单调递增区间为(
, +∞),单调递减区间为(0,
)
(Ⅱ)∵函数g(x)=2f (x)-blnx+x在x∈[1,+∞)上存在零点,
∴方程2xlnx-blnx+x=0在x∈[1,+∞)上有实数解.
易知x=1不是方程的实数解,
∴方程2xlnx-blnx+x=0在x∈(1,+∞)上有实数解,
即方程b=2x+
在x∈(1,+∞)上有实数解.
设ϕ(x)=2x+
(x>1),ϕ′(x)=2+
=
=
,
∵x>1,∴lnx>0,lnx+1>0,
当2lnx-1>0,即x>
时,ϕ'(x)>0;
当2lnx-1<0,即1<x<
时,ϕ'(x)<0,
∴ϕ(x)在(1,
)上单调递减,在(
, +∞)上单调递增,
∴[ϕ(x)]min=ϕ(
)=4
,
∴实数b的取值范围为[4
, +∞).
(Ⅲ)∵存在x0>0使f′(x0)=
成立,
∴lnx 0+1=
成立.
要证明:x0>x1 成立,
只需证明 lnx0+1>lnx1+1成立,
只需证明
>lnx1+1成立,
只需证明 x2(lnx2-lnx1)>x2-x1成立,
只需证明 ln
>1-
成立.
设
=t,∵x1<x2,∴t>1,∴即证明:lnt>1-
当t>1时成立.
令 h(t)=lnt+
-1(t>1),
∵h′(t)=
>0,
∴h(t)在(1,+∞)上单调递增,
∴h(t)>h(1)=0,即 lnt>1-
成立,
∴不等式 x0>x1成立.
由lnx+1>0,即x>
| 1 |
| e |
| 1 |
| e |
由lnx+1<0,即0<x<
| 1 |
| e |
| 1 |
| e |
∴函数f(x)的单调递增区间为(
| 1 |
| e |
| 1 |
| e |
(Ⅱ)∵函数g(x)=2f (x)-blnx+x在x∈[1,+∞)上存在零点,
∴方程2xlnx-blnx+x=0在x∈[1,+∞)上有实数解.
易知x=1不是方程的实数解,
∴方程2xlnx-blnx+x=0在x∈(1,+∞)上有实数解,
即方程b=2x+
| x |
| lnx |
设ϕ(x)=2x+
| x |
| lnx |
| lnx-1 |
| (lnx)2 |
| 2(lnx)2+lnx-1 |
| (lnx)2 |
| (2lnx-1)(lnx+1) |
| (lnx)2 |
∵x>1,∴lnx>0,lnx+1>0,
当2lnx-1>0,即x>
| e |
当2lnx-1<0,即1<x<
| e |
∴ϕ(x)在(1,
| e |
| e |
∴[ϕ(x)]min=ϕ(
| e |
| e |
∴实数b的取值范围为[4
| e |
(Ⅲ)∵存在x0>0使f′(x0)=
| f(x2)-f(x1) |
| x2-x1 |
∴lnx 0+1=
| x2lnx2-x1lnx1 |
| x2-x1 |
要证明:x0>x1 成立,
只需证明 lnx0+1>lnx1+1成立,
只需证明
| x2lnx2-x1lnx1 |
| x2-x1 |
只需证明 x2(lnx2-lnx1)>x2-x1成立,
只需证明 ln
| x2 |
| x1 |
| x1 |
| x2 |
设
| x2 |
| x1 |
| 1 |
| t |
令 h(t)=lnt+
| 1 |
| t |
∵h′(t)=
| t-1 |
| t2 |
∴h(t)在(1,+∞)上单调递增,
∴h(t)>h(1)=0,即 lnt>1-
| 1 |
| t |
∴不等式 x0>x1成立.
点评:本题考查了利用导数研究函数的单调性,考查了通过构造函数,利用函数的单调性和极值证明不等式,是一道难度较大的综合题型.

练习册系列答案
相关题目
数列{an}定义如下:a1=1,且当n≥2时,an=
,若an=
,则正整数n=( )
|
| 19 |
| 11 |
| A、112 | B、114 |
| C、116 | D、118 |
在同一直角坐标系中,函数f(x)=logax(a>0,a≠1)与函数g(x)=ax(a>0,a≠1)的图象可能是( )
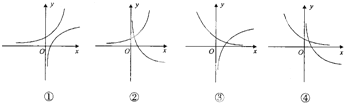

| A、①② | B、①③ | C、①④ | D、②④ |