题目内容
下列函数在(1,+∞)上为增函数的是( )
| A、y=-|x-1| | ||
B、y=x+
| ||
C、y=
| ||
| D、y=x(2-x) |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:举反例说明A,B在(1,+∞)上不是增函数,由二次函数的性质说明y=x(2-x)在(1,+∞)上不是增函数,利用函数单调性的定义证明函数y=
在(1,+∞)上为增函数.
| 3x+1 |
| x+1 |
解答:
解:对于函数y=f(x)=-|x-1|,
∵f(2)=-1,f(3)=-2,f(3)<f(2),
∴y=-|x-1|在(1,+∞)上不是增函数;
对于y=f(x)=x+
,
∵f(
)=
,f(
)=
,f(
)<(
),
∴y=x+
在(1,+∞)上不是增函数;
对于y=x(2-x)=-x2+2x,图象是开口向下的抛物线,对称轴方程为x=1,
在(1,+∞)上为减函数;
对于y=
,在(1,+∞)上任取两个实数x1,x2,
设x1<x2,
则f(x1)-f(x2)=
-
=
=
.
∵x1,x2∈(1,+∞),且x1<x2,
∴
<0,
即f(x1)-f(x2)<0,f(x1)<f(x2).
∴y=
在(1,+∞)上为增函数.
故选:C.
∵f(2)=-1,f(3)=-2,f(3)<f(2),
∴y=-|x-1|在(1,+∞)上不是增函数;
对于y=f(x)=x+
| 2 |
| x |
∵f(
| 5 |
| 4 |
| 57 |
| 2 |
| 3 |
| 2 |
| 17 |
| 6 |
| 3 |
| 2 |
| 5 |
| 4 |
∴y=x+
| 2 |
| x |
对于y=x(2-x)=-x2+2x,图象是开口向下的抛物线,对称轴方程为x=1,
在(1,+∞)上为减函数;
对于y=
| 3x+1 |
| x+1 |
设x1<x2,
则f(x1)-f(x2)=
| 3x1+1 |
| x1+1 |
| 3x2+1 |
| x2+1 |
| 3x1x2+x2+3x1+1-3x1x2-x1-3x2-1 |
| (x1+1)(x2+1) |
=
| 2(x1-x2) |
| (x1+1)(x2+1) |
∵x1,x2∈(1,+∞),且x1<x2,
∴
| 2(x1-x2) |
| (x1+1)(x2+1) |
即f(x1)-f(x2)<0,f(x1)<f(x2).
∴y=
| 3x+1 |
| x+1 |
故选:C.
点评:本题考查了函数单调性的判断与证明,关键是掌握单调性证明的步骤,是基础题.

练习册系列答案
相关题目
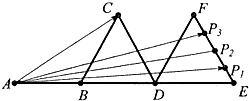 如图,△DBC,△DEF为边长为2的等边三角形,若AB=2,且P1,P2,P3是线段EF上的四等分点,则
如图,△DBC,△DEF为边长为2的等边三角形,若AB=2,且P1,P2,P3是线段EF上的四等分点,则 如图,设AD是△ABC的角平分线,AD交△ABC的外接圆与点E.求证:AB•AC=AD•AE.
如图,设AD是△ABC的角平分线,AD交△ABC的外接圆与点E.求证:AB•AC=AD•AE.